搜索
7. 在平面直角坐标系xOy中,点P(5,-1)关于y轴对称的点的坐标是______.
答案：
$(-5,-1)$
8. 已知点P(2-a,3a+6)在第一象限,且点P到两坐标轴的距离相等,则a= ______.
答案：
$-1$
9. 若$√{a-3}+(b+2)^2= 0,$则点M(a,b)关于y轴的对称点的坐标为______.
答案：
$(-3,-2)$
10. 如图,△COD是由△AOB放大得到的,各点坐标分别为A(1,2),B(3,0),D(4,0),则点C坐标为______.
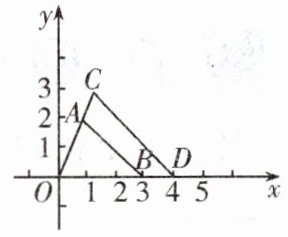
答案：
$(\frac{4}{3},\frac{8}{3})$
11. (14分)如图所示,写出平面直角坐标系中点A,B,C,D,E的坐标.
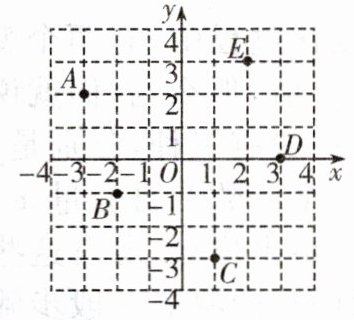
答案：
解：$A(-3,2)$，$B(-2,-1)$，$C(1,-3)$，$D(3,0)$，$E(2,3)$。
12. (14分)已知点P(8-2m,m+1).
(1)若点P在y轴上,求m的值.
(2)若点P在第一象限,且点P到x轴的距离是到y轴距离的2倍,求P点的坐标.
(1)若点P在y轴上,求m的值.
(2)若点P在第一象限,且点P到x轴的距离是到y轴距离的2倍,求P点的坐标.
答案：
解：
(1)因为点$P(8-2m,m+1)$在$y$轴上，所以$8-2m=0$，解得$m=4$。
(2)由题意，可得$m+1=2(8-2m)$，解得$m=3$。则$8-2m=2$，$m+1=4$，故$P(2,4)$。
(1)因为点$P(8-2m,m+1)$在$y$轴上，所以$8-2m=0$，解得$m=4$。
(2)由题意，可得$m+1=2(8-2m)$，解得$m=3$。则$8-2m=2$，$m+1=4$，故$P(2,4)$。
13. (14分)(1)在如图所示的平面直角坐标系中描出下列各点A(1,2),B(-3,3),C(1,3),D(-1,3),E(1,-4),F(3,3)(小方格的边长为1). 由描出的点你发现了什么规律？
(2)应用：已知P(m,-2),Q(3,m-1),且PQ//x轴,求线段PQ的长.
(2)应用：已知P(m,-2),Q(3,m-1),且PQ//x轴,求线段PQ的长.
答案：
解：
(1)描点如图所示：
规律：纵坐标相同的点在平行于$x$轴的直线上，横坐标相同的点在平行于$y$轴的直线上。
(2)因为$PQ// x$轴，所以$m-1=-2$。所以$m=-1$，所以$P(-1,-2)$，$Q(3,-2)$，所以$PQ=∣-1-3∣=4$，所以线段$PQ$的长为$4$。
解：
(1)描点如图所示：
规律：纵坐标相同的点在平行于$x$轴的直线上，横坐标相同的点在平行于$y$轴的直线上。(2)因为$PQ// x$轴，所以$m-1=-2$。所以$m=-1$，所以$P(-1,-2)$，$Q(3,-2)$，所以$PQ=∣-1-3∣=4$，所以线段$PQ$的长为$4$。
14. (14分)如图所示,在平面直角坐标系中,A(-1,5),B(-1,0),C(-4,3).
(1)求△ABC的面积.
(2)画出△ABC向下平移2个单位长度,再向右平移5个单位长度后得到的△A'B'C',并写出C'的坐标.
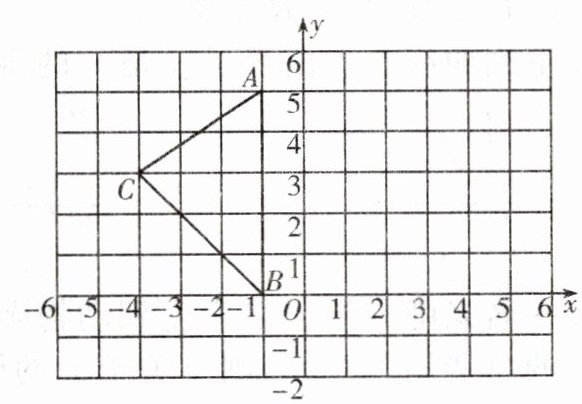
(1)求△ABC的面积.
(2)画出△ABC向下平移2个单位长度,再向右平移5个单位长度后得到的△A'B'C',并写出C'的坐标.
答案：
解：
(1)$\triangle ABC$的面积是$\frac{1}{2}×3×5=7.5$。
(2)作图如下：
所以点$C'$的坐标为$(1,1)$。
解：
(1)$\triangle ABC$的面积是$\frac{1}{2}×3×5=7.5$。
(2)作图如下：
所以点$C'$的坐标为$(1,1)$。 查看更多完整答案，请扫码查看
