《2025年暑假生活新疆文化出版社八年级数学冀教版》

12. (本小题满分14分)
如图,$AC$,$AD$,$CE是正五边形ABCDE$的对角线,$AD与CE相交于点F$,试证明：$CE平分\angle ACD$。

答案： 证明：$\because$ 五边形 $ABCDE$ 是正五边形，$\therefore \angle B = \angle BAE = \angle AED = 108^{\circ}$，$BA = BC$，$EA = ED$，$\therefore \angle BAC = \angle BCA = \angle EAD = \angle EDA = 36^{\circ}$，$\therefore \angle CAD = 36^{\circ}$，又 $AC = AD$，$\therefore \angle ACD = \angle ADC = 72^{\circ}$，在 $\triangle CDE$ 中，$\angle CDE = 108^{\circ}$，$CD = DE$，$\therefore \angle DCE = \angle DEC = 36^{\circ}$，$\therefore \angle DCE = \frac{1}{2}\angle ACD$，即 $CE$ 平分 $\angle ACD$。

13. (本小题满分14分)
在学习了平行四边形后,小虹进行了拓展性研究。她发现,如果作平行四边形一条对角线的垂直平分线,那么这个平行四边形的一组对边截垂直平分线所得的线段被垂足平分。她的解决思路是通过证明对应线段所在的两个三角形全等得出结论。请根据她的思路完成以下作图与填空：
用直尺和圆规,作$AC的垂直平分线交DC于点E$,交$AB于点F$,垂足为点$O$。(只保留作图痕迹)
已知：如图,四边形$ABCD$是平行四边形,$AC$是对角线,$EF垂直平分AC$,垂足为点$O$。
求证：$OE= OF$。
证明：$\because四边形ABCD$是平行四边形,
$\therefore DC// AB$。
$\therefore \angle ECO= $______①______。
$\because EF垂直平分AC$,
$\therefore$______②______。
又$\angle EOC= $______③______,
$\therefore \triangle COE\cong\triangle AOF(ASA)$。
$\therefore OE= OF$。
再进一步研究发现,过平行四边形对角线$AC$中点的直线与平行四边形一组对边相交形成的线段均有此特征。请你依照题意完成下面命题的填空：
过平行四边形对角线中点的直线______④______。

答案：
解：作图如图；① $\angle FAO$；② $OA = OC$；③ $\angle FOA$；④ 与其一组对边相交所得的线段被对角线平分。

14. (本小题满分14分)
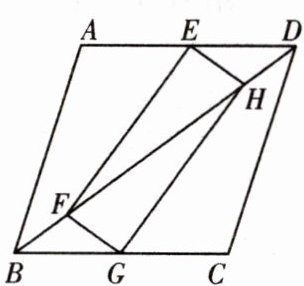
如图,矩形$EFGH的顶点E$,$G分别在菱形ABCD的边AD$,$BC$上,顶点$F$,$H在菱形ABCD的对角线BD$上。
(1)求证：$BG= DE$；
(2)若$E为AD$的中点,$FH= 2$,求菱形$ABCD$的周长。

答案： 解：
(1) 证明：在矩形 $EFGH$ 中，$\because EH = FG$，$EH // FG$，$\therefore \angle GFH = \angle EHF$。$\because \angle BFG = 180^{\circ} - \angle GFH$，$\angle DHE = 180^{\circ} - \angle EHF$，$\therefore \angle BFG = \angle DHE$。$\because$ 在菱形 $ABCD$ 中，$AD // BC$，$\therefore \angle GBF = \angle EDH$，$\therefore \triangle BGF \cong \triangle EDH$（AAS），$\therefore BG = DE$。
(2) 连接 $EG$。在菱形 $ABCD$ 中，$AD // BC$。$\because E$ 为 $AD$ 中点，$\therefore AE = DE$。$\because BG = DE$，$\therefore AE = BG$，$\therefore$ 四边形 $ABGE$ 为平行四边形，$\therefore AB = EG$。$\because$ 在矩形 $EFGH$ 中，$EG = FH = 2$，$\therefore AB = 2$，$\therefore$ 菱形 $ABCD$ 的周长为 8。