《2025年暑假生活新疆文化出版社八年级数学冀教版》

12. (14分)一辆汽车的油箱中现有汽油50 L.若不再加油,则油箱中的剩余油量y(单位:L)随行驶里程x(单位:km)的增加而减少,平均每千米的耗油量为0.1 L.
(1)求出y关于x的函数表达式,写出自变量x的取值范围;
(2)画出这个函数的图象;
(3)汽车行驶200 km时,油箱中还有多少油?
(4)汽车最多可行驶多少千米?

答案：
(1) $ y = 50 - 0.1x $，$ 0 \leq x \leq 500 $
(2) 画图象时，横轴 1 格表示 100，纵轴 1 格表示 10，图象略
(3) 30L
(4) 500 千米

13. (14分)某剧院的观众席座位为扇形,且按下列方式设置:
|排数(x)|1|2|3|4|…|
|座位数(y)|50|53|56|59|…|
(1)按照上表所示的规律,当x每增加1时,y如何变化;
(2)写出座位数y与排数x间的关系式;
(3)按照上表所示的规律,某一排可能有90个座位吗? 说说你的理由.

答案：
(1) 由图表中数据可得：当 $ x $ 每增加 1 时，$ y $ 增加 3.
(2) 由题意，得 $ y = 50 + 3(x - 1) = 3x + 47 $.
(3) 某一排不可能有 90 个座位. 理由：由题意，得 $ y = 3x + 47 = 90 $，解得 $ x = \frac{43}{3} $，$ x $ 不是整数，故某一排不可能有 90 个座位.

14. (14分)小明从家出发骑自行车去上学,当他以往常的速度骑了一段路后,突然想起要买文具,于是又折回到刚经过的某文具店,买到文具后继续骑车去学校.如图是他本次上学离家的距离与所用时间的变化情况的图象.根据图中提供的信息回答下列问题:
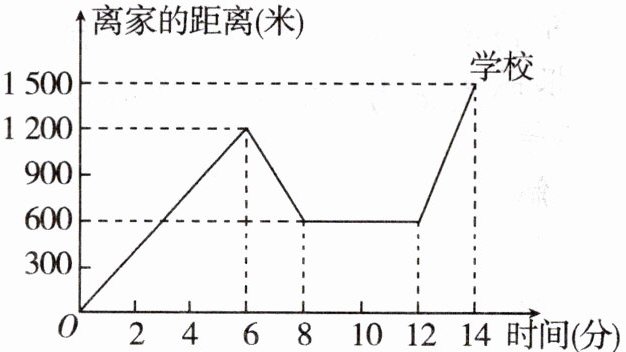
(1)小明家到学校的距离是____米,文具店到学校的距离是____米.
(2)小明在文具店停留了____分钟,本次上学途中,小明一共行驶了____米.
(3)在整个上学途中,哪个时间段小明骑车速度最快? 最快的速度是多少?
(4)如果小明不买文具,以往常的速度去学校,需要花费多长时间? 本次上学比往常多用了多长时间?

答案：
(1) 1500 900
(2) 4 2700
(3) 根据题中图象，可知第 12 分钟至 14 分钟这一段时间段的线段最陡，所以小明在第 12 分钟至 14 分钟这一时间段的骑车速度最快，此时速度为 $ \frac{1500 - 600}{14 - 12} = 450 $（米/分）
(4) 小明往常的速度为 $ 1200 ÷ 6 = 200 $（米/分），去学校需要花费的时间为 $ 1500 ÷ 200 = 7.5 $（分），本次上学共用了 14 分钟，比往常多用的时间为 $ 14 - 7.5 = 6.5 $（分）