《2025年1课3练单元达标测试四年级数学上册苏教版》

例：$440 - 200 ÷ 5 × 8$ $55 ÷ 5 + 48 ÷ 6$

答案： 解析：
这两道题目都是基础的四则运算题目，需要遵循运算的优先级，即先乘除后加减，有括号先算括号里的。
第一题 $440 - 200 ÷ 5 × 8$ 需要先算除法，再算乘法，最后算减法。
第二题 $55 ÷ 5 + 48 ÷ 6$ 需要同时算两个除法，然后再算加法。
答案：
第一题：
$440 - 200 ÷ 5 × 8$
$= 440 - 40 × 8$
$= 440 - 320$
$= 120$
第二题：
$55 ÷ 5 + 48 ÷ 6$
$= 11 + 8$
$= 19$

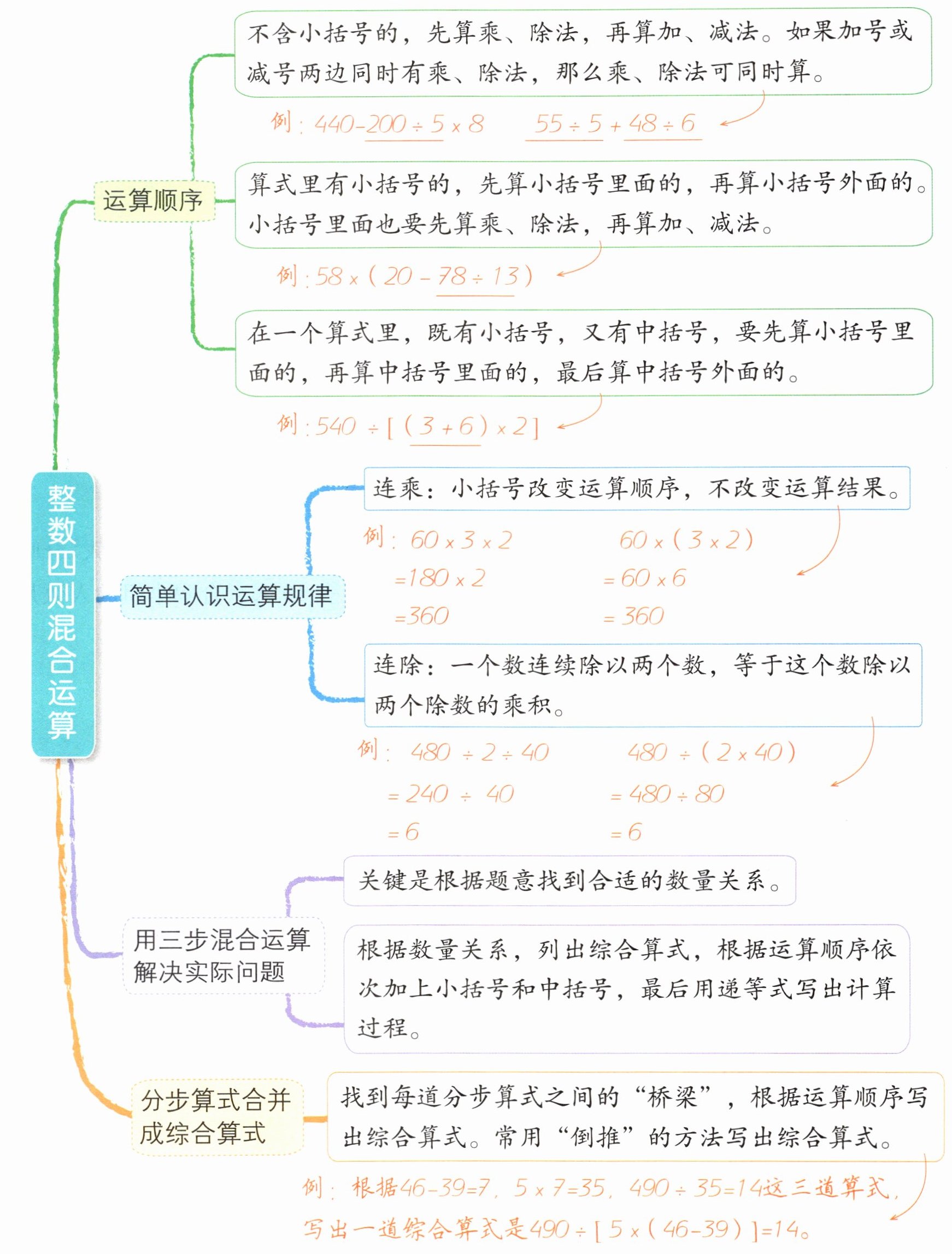
算式里有小括号的,先算小括号里面的,再算小括号外面的。小括号里面也要先算乘、除法,再算加、减法。
例：$58 × (20 - 78 ÷ 13)$
在一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的,最后算中括号外面的。
例：$540 ÷ [(3 + 6) × 2]$
简单认识运算规律
连乘：小括号改变运算顺序,不改变运算结果。
例：$60 × 3 × 2$　　　$60 × (3 × 2)$
$= 180 × 2$　　　$= 60 × 6$
$= 360$　　　$= 360$
连除：一个数连续除以两个数,等于这个数除以两个除数的乘积。
例：$480 ÷ 2 ÷ 40$　　　$480 ÷ (2 × 40)$
$= 240 ÷ 40$　　　$= 480 ÷ 80$
$= 6$　　　$= 6$
用三步混合运算解决实际问题
关键是根据题意找到合适的数量关系。
根据数量关系,列出综合算式,根据运算顺序依次加上小括号和中括号,最后用递等式写出计算过程。
分步算式合并成综合算式
找到每道分步算式之间的“桥梁”,根据运算顺序写出综合算式。常用“倒推”的方法写出综合算式。
例：根据$46 - 39 = 7$,$5 × 7 = 35$,$490 ÷ 35 = 14$这三道算式,写出一道综合算式是$490 ÷ [5 × (46 - 39)] = 14$。

答案： 解析：本题主要考查了整数四则混合运算的运算顺序、运算规律以及用三步混合运算解决实际问题和分步算式合并成综合算式的知识点。
答案不唯一，示例如下：
一、运算顺序
不含小括号的，先算乘、除法，再算加、减法。如果加号或减号两边同时有乘、除法，那么乘、除法可同时算。
例：$440 - 200÷5×8$
$=440 - 40×8$
$=440 - 320$
$= 120$
$55÷5 + 48÷6$
$=11 + 8$
$= 19$
算式里有小括号的，先算小括号里面的，再算小括号外面的。小括号里面也要先算乘、除法，再算加、减法。
例：$58×(20 - 78÷13)$
$=58×(20 - 6)$
$=58×14$
$= 812$
在一个算式里，既有小括号，又有中括号，要先算小括号里面的，再算中括号里面的，最后算中括号外面的。
例：$540÷[(3 + 6)×2]$
$=540÷[9×2]$
$=540÷18$
$= 30$
二、简单认识运算规律
连乘：小括号改变运算顺序，不改变运算结果。
例：$60×3×2$
$=180×2$
$= 360$
$60×(3×2)$
$=60×6$
$= 360$
连除：一个数连续除以两个数，等于这个数除以两个除数的乘积。
例：$480÷2÷40$
$= 240÷40$
$= 6$
$480÷(2×40)$
$=480÷80$
$= 6$
三、用三步混合运算解决实际问题
关键是根据题意找到合适的数量关系。根据数量关系，列出综合算式，根据运算顺序依次加上小括号和中括号，最后用递等式写出计算过程。
四、分步算式合并成综合算式
找到每道分步算式之间的“桥梁”，根据运算顺序写出综合算式。常用“倒推”的方法写出综合算式。
例：根据$46 - 39 = 7$，$5×7 = 35$，$490÷35 = 14$这三道算式，写出一道综合算式是$490÷[5×(46 - 39)] = 14$。

算式里有小括号的,先算小括号里面的,再算小括号外面的。小括号里面也要先算乘、除法,再算加、减法。
例：$58 × (20 - 78 ÷ 13)$
在一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的,最后算中括号外面的。
例：$540 ÷ [(3 + 6) × 2]$
简单认识运算规律
连乘：小括号改变运算顺序,不改变运算结果。
例：$60 × 3 × 2$　　　$60 × (3 × 2)$
$= 180 × 2$　　　$= 60 × 6$
$= 360$　　　$= 360$
连除：一个数连续除以两个数,等于这个数除以两个除数的乘积。
例：$480 ÷ 2 ÷ 40$　　　$480 ÷ (2 × 40)$
$= 240 ÷ 40$　　　$= 480 ÷ 80$
$= 6$　　　$= 6$
用三步混合运算解决实际问题
关键是根据题意找到合适的数量关系。
根据数量关系,列出综合算式,根据运算顺序依次加上小括号和中括号,最后用递等式写出计算过程。
分步算式合并成综合算式
找到每道分步算式之间的“桥梁”,根据运算顺序写出综合算式。常用“倒推”的方法写出综合算式。
例：根据$46 - 39 = 7$,$5 × 7 = 35$,$490 ÷ 35 = 14$这三道算式,写出一道综合算式是$490 ÷ [5 × (46 - 39)] = 14$。

答案： 解析：本题主要考查了整数四则混合运算的运算顺序、运算规律以及用三步混合运算解决实际问题和分步算式合并成综合算式的方法。
答案不唯一，示例如下：
一、运算顺序
不含小括号的，先算乘、除法，再算加、减法。如果加号或减号两边同时有乘、除法，那么乘、除法可同时算。
例：$440 - 200÷5×8$
$=440 - 40×8$
$=440 - 320$
$= 120$
$55÷5 + 48÷6$
$=11 + 8$
$= 19$
算式里有小括号的，先算小括号里面的，再算小括号外面的。小括号里面也要先算乘、除法，再算加、减法。
例：$58×(20 - 78÷13)$
$=58×(20 - 6)$
$=58×14$
$= 812$
在一个算式里，既有小括号，又有中括号，要先算小括号里面的，再算中括号里面的，最后算中括号外面的。
例：$540÷[(3 + 6)×2]$
$=540÷[9×2]$
$=540÷18$
$= 30$
二、简单认识运算规律
连乘：小括号改变运算顺序，不改变运算结果。
例：$60×3×2$
$=180×2$
$= 360$
$60×(3×2)$
$=60×6$
$= 360$
连除：一个数连续除以两个数，等于这个数除以两个除数的乘积。
例：$480÷2÷40$
$= 240÷40$
$= 6$
$480÷(2×40)$
$=480÷80$
$= 6$
三、用三步混合运算解决实际问题
关键是根据题意找到合适的数量关系。根据数量关系，列出综合算式，根据运算顺序依次加上小括号和中括号，最后用递等式写出计算过程。
四、分步算式合并成综合算式
找到每道分步算式之间的“桥梁”，根据运算顺序写出综合算式。常用“倒推”的方法写出综合算式。
例：根据$46 - 39 = 7$，$5×7 = 35$，$490÷35 = 14$这三道算式，写出一道综合算式是$490÷[5×(46 - 39)] = 14$。

算式里有小括号的,先算小括号里面的,再算小括号外面的。小括号里面也要先算乘、除法,再算加、减法。
例：$58 × (20 - 78 ÷ 13)$
在一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的,最后算中括号外面的。
例：$540 ÷ [(3 + 6) × 2]$
简单认识运算规律
连乘：小括号改变运算顺序,不改变运算结果。
例：$60 × 3 × 2$　　　$60 × (3 × 2)$
$= 180 × 2$　　　$= 60 × 6$
$= 360$　　　$= 360$
连除：一个数连续除以两个数,等于这个数除以两个除数的乘积。
例：$480 ÷ 2 ÷ 40$　　　$480 ÷ (2 × 40)$
$= 240 ÷ 40$　　　$= 480 ÷ 80$
$= 6$　　　$= 6$
用三步混合运算解决实际问题
关键是根据题意找到合适的数量关系。
根据数量关系,列出综合算式,根据运算顺序依次加上小括号和中括号,最后用递等式写出计算过程。
分步算式合并成综合算式
找到每道分步算式之间的“桥梁”,根据运算顺序写出综合算式。常用“倒推”的方法写出综合算式。
例：根据$46 - 39 = 7$,$5 × 7 = 35$,$490 ÷ 35 = 14$这三道算式,写出一道综合算式是$490 ÷ [5 × (46 - 39)] = 14$。

答案： 解析：本题主要考查了整数四则混合运算的运算顺序、运算规律以及用三步混合运算解决实际问题和分步算式合并成综合算式。
答案：运算顺序：
不含小括号的，先算乘、除法，再算加、减法。如果加号或减号两边同时有乘、除法，那么乘、除法可同时算。例如$440 - 200÷5×8$ ，$55÷5 + 48÷6$。
算式里有小括号的，先算小括号里面的，再算小括号外面的。小括号里面也要先算乘、除法，再算加、减法。例如$58×(20 - 78÷13)$ 。
在一个算式里，既有小括号，又有中括号，要先算小括号里面的，再算中括号里面的，最后算中括号外面的。例如$540÷[(3 + 6)×2]$ 。
简单认识运算规律：
连乘：小括号改变运算顺序，不改变运算结果。例如$60×3×2$ ，$60×(3×2)$ ，结果都为$360$ 。
连除：一个数连续除以两个数，等于这个数除以两个除数的乘积。例如$480÷2÷40$ ，$480÷(2×40)$ ，结果都为$6$ 。
用三步混合运算解决实际问题：关键是根据题意找到合适的数量关系，根据数量关系，列出综合算式，根据运算顺序依次加上小括号和中括号，最后用递等式写出计算过程。
分步算式合并成综合算式：找到每道分步算式之间的“桥梁”，根据运算顺序写出综合算式。常用“倒推”的方法写出综合算式。例如根据$46 - 39 = 7$ ，$5×7 = 35$ ，$490÷35 = 14$这三道算式，写出一道综合算式是$490÷[5×(46 - 39)] = 14$ 。

算式里有小括号的,先算小括号里面的,再算小括号外面的。小括号里面也要先算乘、除法,再算加、减法。
例：$58 × (20 - 78 ÷ 13)$
在一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的,最后算中括号外面的。
例：$540 ÷ [(3 + 6) × 2]$
简单认识运算规律
连乘：小括号改变运算顺序,不改变运算结果。
例：$60 × 3 × 2$　　　$60 × (3 × 2)$
$= 180 × 2$　　　$= 60 × 6$
$= 360$　　　$= 360$
连除：一个数连续除以两个数,等于这个数除以两个除数的乘积。
例：$480 ÷ 2 ÷ 40$　　　$480 ÷ (2 × 40)$
$= 240 ÷ 40$　　　$= 480 ÷ 80$
$= 6$　　　$= 6$
用三步混合运算解决实际问题
关键是根据题意找到合适的数量关系。
根据数量关系,列出综合算式,根据运算顺序依次加上小括号和中括号,最后用递等式写出计算过程。
分步算式合并成综合算式
找到每道分步算式之间的“桥梁”,根据运算顺序写出综合算式。常用“倒推”的方法写出综合算式。
例：根据$46 - 39 = 7$,$5 × 7 = 35$,$490 ÷ 35 = 14$这三道算式,写出一道综合算式是$490 ÷ [5 × (46 - 39)] = 14$。

答案： 本题主要考查了整数四则混合运算的运算顺序、运算规律以及用混合运算解决实际问题和分步算式合并成综合算式等知识点。
解析：
运算顺序：
不含小括号的，先算乘、除法，再算加、减法。如果加号或减号两边同时有乘、除法，那么乘、除法可同时算。
算式里有小括号的，先算小括号里面的，再算小括号外面的。小括号里面也要先算乘、除法，再算加、减法。
在一个算式里，既有小括号，又有中括号，要先算小括号里面的，再算中括号里面的，最后算中括号外面的。
简单认识运算规律：
连乘：小括号改变运算顺序，不改变运算结果。
连除：一个数连续除以两个数，等于这个数除以两个除数的乘积。
用三步混合运算解决实际问题：
关键是根据题意找到合适的数量关系。
根据数量关系，列出综合算式，根据运算顺序依次加上小括号和中括号，最后用递等式写出计算过程。
分步算式合并成综合算式：
找到每道分步算式之间的“桥梁”，根据运算顺序写出综合算式。常用“倒推”的方法写出综合算式。
答案：
运算顺序：
不含小括号：先乘除，后加减；乘除同时有，可同时算。
有小括号：先算小括号内，乘除优先加减。
既有小括号又有中括号：先小括号，再中括号，最后括号外。
简单认识运算规律：
连乘：$(a× b)× c=a×(b× c)$。
连除：$a÷ b÷ c=a÷(b× c)$。
用三步混合运算解决实际问题：
根据题意找数量关系，列综合算式，加括号，写计算过程。
分步算式合并成综合算式：
找“桥梁”，按运算顺序写综合算式，可用“倒推”法。

算式里有小括号的,先算小括号里面的,再算小括号外面的。小括号里面也要先算乘、除法,再算加、减法。
例：$58 × (20 - 78 ÷ 13)$
在一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的,最后算中括号外面的。
例：$540 ÷ [(3 + 6) × 2]$
简单认识运算规律
连乘：小括号改变运算顺序,不改变运算结果。
例：$60 × 3 × 2$　　　$60 × (3 × 2)$
$= 180 × 2$　　　$= 60 × 6$
$= 360$　　　$= 360$
连除：一个数连续除以两个数,等于这个数除以两个除数的乘积。
例：$480 ÷ 2 ÷ 40$　　　$480 ÷ (2 × 40)$
$= 240 ÷ 40$　　　$= 480 ÷ 80$
$= 6$　　　$= 6$
用三步混合运算解决实际问题
关键是根据题意找到合适的数量关系。
根据数量关系,列出综合算式,根据运算顺序依次加上小括号和中括号,最后用递等式写出计算过程。
分步算式合并成综合算式
找到每道分步算式之间的“桥梁”,根据运算顺序写出综合算式。常用“倒推”的方法写出综合算式。
例：根据$46 - 39 = 7$,$5 × 7 = 35$,$490 ÷ 35 = 14$这三道算式,写出一道综合算式是$490 ÷ [5 × (46 - 39)] = 14$。

答案： 解析：本题主要考查了整数四则混合运算的运算顺序、运算规律以及用三步混合运算解决实际问题和分步算式合并成综合算式的方法。
答案：整数四则混合运算的运算顺序为：不含小括号的，先算乘、除法，再算加、减法。如果加号或减号两边同时有乘、除法，那么乘、除法可同时算；算式里有小括号的，先算小括号里面的，再算小括号外面的。小括号里面也要先算乘、除法，再算加、减法；在一个算式里，既有小括号，又有中括号，要先算小括号里面的，再算中括号里面的，最后算中括号外面的。
运算规律有：连乘时，小括号改变运算顺序，不改变运算结果，如$60×3×2 = 60×(3×2)=360$；连除时，一个数连续除以两个数，等于这个数除以两个除数的乘积，如$480÷2÷40 = 480÷(2×40)=6$。
用三步混合运算解决实际问题的关键是根据题意找到合适的数量关系，根据数量关系列出综合算式，根据运算顺序依次加上小括号和中括号，最后用递等式写出计算过程。
分步算式合并成综合算式要找到每道分步算式之间的“桥梁”，根据运算顺序写出综合算式，常用“倒推”的方法写出综合算式，例如根据$46 - 39 = 7$，$5×7 = 35$，$490÷35 = 14$这三道算式，写出一道综合算式是$490÷[5×(46 - 39)] = 14$。