1 如图,已知∠1= ∠2,若用“SAS”证明△BDA≌△ACB,还需加上条件 ( )

A.AD= BC
B.∠D= ∠C
C.BD= AC
D.OA= OB

A.AD= BC
B.∠D= ∠C
C.BD= AC
D.OA= OB
答案:
C
2 如图,在△ABC中,D为边BC的中点,AB= 1,AD= 2,延长AD至点E,使得DE= AD,则AC的长度可以是 ( )
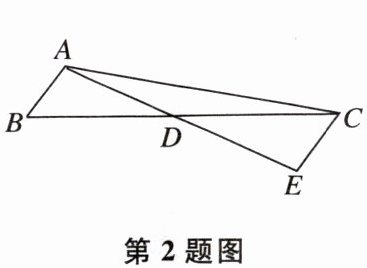
A.4
B.5
C.6
D.7

A.4
B.5
C.6
D.7
答案:
A
3 如图,在△ABC中,D是AB上一点,DF交AC于点E,DE= EF,AE= EC,给出下列结论,①∠ADE= ∠EFC;②∠ADE+∠ECF+∠FEC= 180°;③∠B+∠BCF= 180°;④S△ABC = S四边形BCFE。其中,正确的结论有 个。
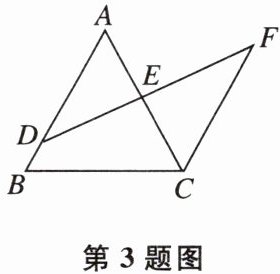

答案:
4 【解析】在△ADE 和△CFE 中,
$\left\{\begin{array}{l} DE=EF,\\ ∠AED=∠CEF,\\ AE=EC,\end{array}\right. $
所以$△ADE\cong △CFE(SAS),$
所以$∠A=∠ACF,∠ADE=∠F,S_{△ADE}=S_{△CFE},$
所以$AD// CF,S_{△ADE}+S_{四边形DBCE}=S_{△CFE}+S_{四边形DBCE},$
所以$∠B+∠BCF=180^{\circ },S_{△ABC}=S_{四边形DBCF}$。
因为$∠F+∠ECF+∠FEC=180^{\circ },$
所以$∠ADE+∠ECF+∠FEC=180^{\circ }$。
综上所述,正确的结论共有 4 个。
$\left\{\begin{array}{l} DE=EF,\\ ∠AED=∠CEF,\\ AE=EC,\end{array}\right. $
所以$△ADE\cong △CFE(SAS),$
所以$∠A=∠ACF,∠ADE=∠F,S_{△ADE}=S_{△CFE},$
所以$AD// CF,S_{△ADE}+S_{四边形DBCE}=S_{△CFE}+S_{四边形DBCE},$
所以$∠B+∠BCF=180^{\circ },S_{△ABC}=S_{四边形DBCF}$。
因为$∠F+∠ECF+∠FEC=180^{\circ },$
所以$∠ADE+∠ECF+∠FEC=180^{\circ }$。
综上所述,正确的结论共有 4 个。
4 如图,已知点A,E,F,D在同一条直线上,若AB//CD,AB= CD,AE= FD。
(1)求证:△BAF≌△CDE。
(2)图中还有哪几对全等三角形?

(1)求证:△BAF≌△CDE。
(2)图中还有哪几对全等三角形?

答案:
(1)证明:因为$AE=DF,$
所以$AE+EF=DF+EF$,所以$AF=DE$。
因为$AB// CD$,所以$∠A=∠D$。
在$△BAF$和$△CDE$中,因为$\left\{\begin{array}{l} AB=DC,\\ ∠A=∠D,\\ AF=DE,\end{array}\right. $
所以$△BAF\cong △CDE(SAS)$。
(2)还有 2 对全等三角形,分别是$△ABE\cong △DCF,△BEF\cong △CFE$。
(1)证明:因为$AE=DF,$
所以$AE+EF=DF+EF$,所以$AF=DE$。
因为$AB// CD$,所以$∠A=∠D$。
在$△BAF$和$△CDE$中,因为$\left\{\begin{array}{l} AB=DC,\\ ∠A=∠D,\\ AF=DE,\end{array}\right. $
所以$△BAF\cong △CDE(SAS)$。
(2)还有 2 对全等三角形,分别是$△ABE\cong △DCF,△BEF\cong △CFE$。
5 如图,在△ABC中,D为AB上一点,E为AC的中点,连结DE并延长至点F,使得EF= ED,连结CF。
(1)求证:CF//AB。
(2)若∠ABC= 50°,连结BE,BE平分∠ABC,CA平分∠BCF,求∠A的度数。
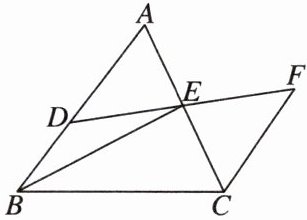
(1)求证:CF//AB。
(2)若∠ABC= 50°,连结BE,BE平分∠ABC,CA平分∠BCF,求∠A的度数。

答案:
(1)证明:因为 E 为 AC 的中点,
所以$AE=CE$。
在$△AED$和$△CEF$中,
因为$\left\{\begin{array}{l} AE=CE,\\ ∠AED=∠CEF,\\ DE=EF,\end{array}\right. $
所以$△AED\cong △CEF(SAS),$
所以$∠A=∠ACF,$
所以$CF// AB$。
(2)因为 CA 平分$∠BCF,$
所以$∠ACB=∠ACF$。
因为$∠A=∠ACF,$
所以$∠A=∠ACB$。
因为$∠A+∠ABC+∠ACB=180^{\circ },∠ABC=50^{\circ },$
所以$2∠A=130^{\circ },$
所以$∠A=65^{\circ }$。
(1)证明:因为 E 为 AC 的中点,
所以$AE=CE$。
在$△AED$和$△CEF$中,
因为$\left\{\begin{array}{l} AE=CE,\\ ∠AED=∠CEF,\\ DE=EF,\end{array}\right. $
所以$△AED\cong △CEF(SAS),$
所以$∠A=∠ACF,$
所以$CF// AB$。
(2)因为 CA 平分$∠BCF,$
所以$∠ACB=∠ACF$。
因为$∠A=∠ACF,$
所以$∠A=∠ACB$。
因为$∠A+∠ABC+∠ACB=180^{\circ },∠ABC=50^{\circ },$
所以$2∠A=130^{\circ },$
所以$∠A=65^{\circ }$。
查看更多完整答案,请扫码查看


