《2025年精彩三年就练这一本八年级数学上册浙教版》

■1在△ABC中,∠C= 90°,∠B= 4∠A,则∠A的度数为( )

A.21°
B.18°
C.15°
D.11.25°

答案： B

■2如图,在Rt△ABC中,CD是斜边AB上的中线,若∠A= 26°,则∠BDC的度数为( )

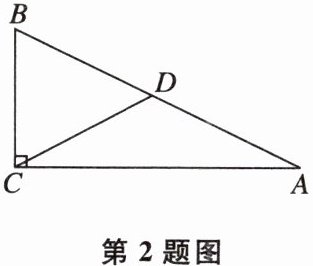
A.26°
B.48°
C.52°
D.64°

答案： C

■3如图,将一个有45°角的三角板的直角顶点放在一张宽为3 cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,则三角板的直角边的长为( )

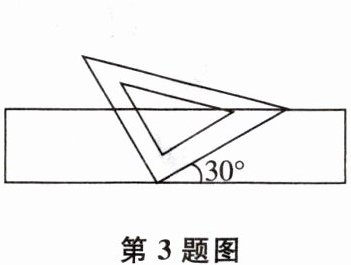
A.3 cm
B.6 cm
C.8 cm
D.9 cm

答案： B

■4如图,在△ABC中,∠ACB= 90°,∠ABC= 60°,BD平分∠ABC,P是BD的中点,若AD= 6,则CP的长为______。

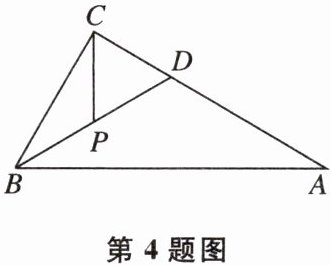
答案： 3 【解析】过点 D 作 DE⊥AB 于 E(图略)，
因为∠ACB=90°,∠ABC=60°，
所以∠A=90°-60°=30°，
所以 DE=$\frac{1}{2}$AD=$\frac{1}{2}$×6=3。
又因为 BD 平分∠ABC，
所以 CD=DE=3。
因为∠ABC=60°,BD 平分∠ABC，
所以∠CBD=30°，
所以 BD=2CD=2×3=6。
因为 P 是 BD 的中点，
所以 CP=$\frac{1}{2}$BD=$\frac{1}{2}$×6=3。

■5如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,点M为BC的中点。
(1)求证：MF= ME。
(2)若∠ABC= 50°,∠ACB= 65°,求∠FME的度数。

答案： 解:
(1)证明:因为 CF⊥AB 于 F,M 为 BC 的中点，
所以 MF=$\frac{1}{2}$BC，
同理 ME=$\frac{1}{2}$BC，
所以 MF=ME。
(2)因为 MF=MB，
所以∠ABC=∠MFB=50°，
同理∠ACB=∠MEC=65°，
所以∠BMF=180°-50°-50°=80°，
∠EMC=180°-65°-65°=50°，
所以∠FME=180°-80°-50°=50°。