《2025年精彩三年就练这一本八年级数学上册浙教版》

1已知等腰三角形有一个角是20°,则顶角的度数为 （ ）

A.20°
B.140°
C.36°
D.20°或140°

答案： D

2在等腰三角形ABC中,∠A=2∠B,则∠C的度数为 （ ）

A.36°
B.45°
C.36°或45°
D.45°或72°

答案： D

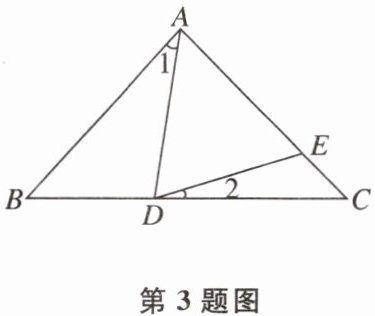
3如图,在△ABC中,AB=AC,AD=AE,则∠1与∠2的关系是 （ ）

A.∠1=2∠2
B.∠1+∠2=90°
C.∠1+2∠2=180°
D.2∠1+∠2=180°

答案： A

4如图,点C,D,E都在∠AOB的边上,OC=CD=DE,若∠BDE=75°,则∠AOB的度数是______°。

答案： 25

5如图,在△ABC中,AB=AC,点D在AC边上(不与A,C重合),连结BD,BD=AB。设∠C=α，∠ABD=β。
(1)当α=50°时,求β。
(2)请求出β与α的数量关系。

答案： 解:
(1)因为AB=AC，
所以∠ABC=∠C=50°，
所以∠A=180°-∠ABC-∠C=80°。
因为BD=AB，
所以∠BDA=∠A=80°，
所以β=180°-∠A-∠BDA=20°。
(2)因为AB=BD，
所以∠A=∠ADB，
所以β=180°-2∠A。
又因为AB=AC，
所以∠ABC=∠C=α，
所以∠A=180°-2∠C=180°-2α，
所以β=180°-2(180°-2α)=4α-180°，
即β=4α-180°。