《2025年精彩三年就练这一本八年级数学上册浙教版》

1 下列生活中的一些事实运用了“三角形稳定性”的是 ( )

答案： C

2 如图,在△ABD和△ACD中,AB= AC,BD= CD,则能说明△ABD≌△ACD的依据是 。

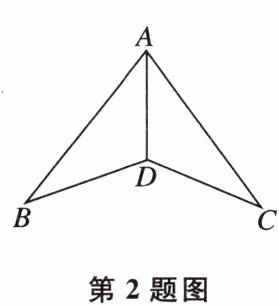
答案： SSS

3 如图,点B,E,C,F在同一条直线上,AB= DE,AC= DF,BE= CF,求证：∠D= ∠A。下面是小红同学的证明过程,请你说明相关步骤的理由。

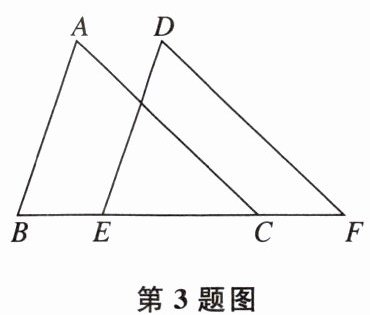
证明：因为 BE= CF,
所以 BE+EC= CF+EC,即 BC= EF。
在△ABC 和△DEF 中,
$\left\{\begin{array}{l} AB= DE,\\ AC= DF,\\ BC= EF,\end{array} \right.$
所以△ABC≌△DEF( ),
所以∠D= ∠A( )。

答案： SSS 全等三角形的对应角相等。

4 如图,点E,F在BD上,且AB= CD,BF= DE,AE= CF,证明：∠B= ∠D。请你在横线上补充其推理过程或理由。

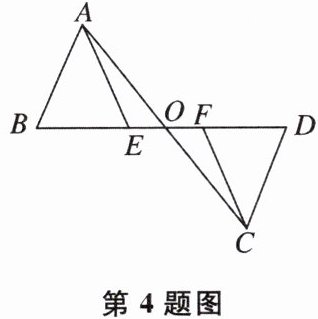
证明：因为 BF= DE,
所以 BF-EF= DE-EF,
即 。
因为 AB= CD,AE= CF,
所以 (SSS),
所以∠B= ∠D( )。

答案： BE=DF △ABE≌△CDF 全等三角形的对应角相等

5 如图,已知AB= AC,AD= AE,BD= CE。
(1)求证：∠BAC= ∠DAE。
(2)写出∠1,∠2,∠3之间的数量关系,并证明。

答案： 解:
(1)证明:在△BAD 和△CAE 中，
因为{AB=AC，
AD=AE，
BD=CE，
所以△BAD≌△CAE(SSS)，
所以∠BAD=∠CAE，
所以∠BAD+∠DAC=∠CAE+∠DAC，
所以∠BAC=∠DAE。
(2)∠3=∠1+∠2。
证明:因为△BAD≌△CAE,所以∠ABD=∠2。
因为∠3=∠1+∠ABD,所以∠3=∠1+∠2。