《2025年精彩三年就练这一本八年级数学上册浙教版》

1 能说明“相等的角是对顶角”为假命题的一个反例是( )

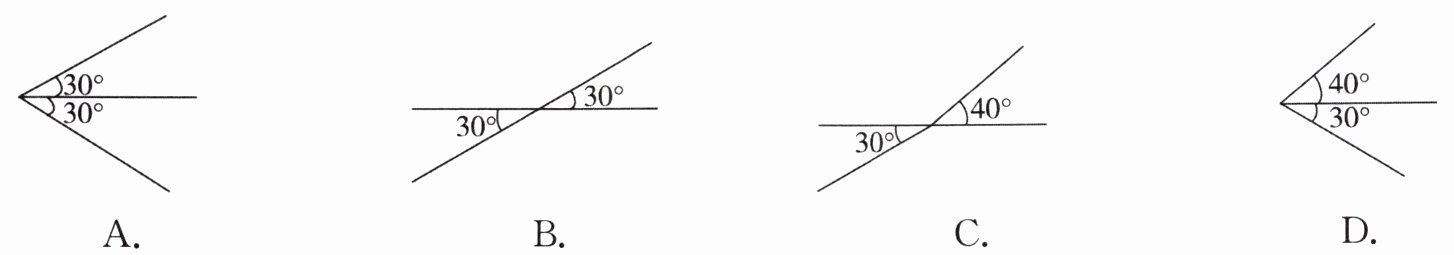
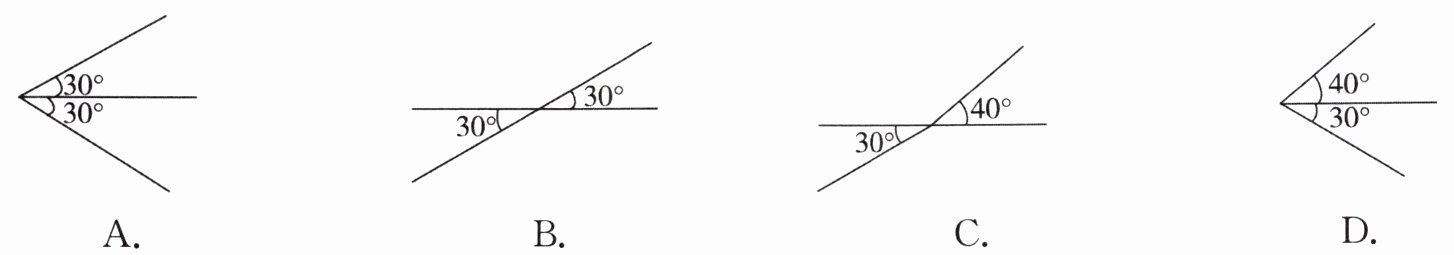
答案： A

2 下列命题中的真命题是( )

A.内错角相等
B.$\pi$是无理数
C.$\sqrt{6}$是有理数
D.若$|a|= 1$,则$a= 1$

答案： B

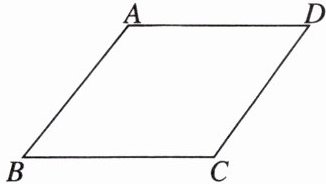
3 如图,给出下列论断:①$AB// CD$。②$AD// BC$。③$\angle A+\angle B= 180^\circ$。④$\angle B+\angle C= 180^\circ$。其中一个作为题设,一个作为结论,写出一个真命题,真命题为 。

答案： 若AB//CD,则∠B+∠C=180°(答案不唯一)

4 有下列说法：
①“三角形的内角和等于$180^\circ$”是命题,也是定理。
②“两点之间线段最短”是命题,也是基本事实。
③“若$a+b= 2$,则$a= b= 1$”是假命题。
其中正确的说法是 。(填序号)

答案： ①②③

5 指出下列命题的条件和结论,并判断它们是真命题还是假命题,如果是假命题,举出一个反例。
(1)两个角的和等于直角时,这两个角互为余角。
(2)同旁内角互补。

答案：
解:
(1)条件:两个角的和等于直角，结论:这两个角互为余角。
这个命题是真命题。

(2)条件:两个角是同旁内角，结论:这两个角互补。
这个命题是假命题。
反例:如图,∠1与∠2是同旁内角,但∠1+∠2≠180°。