《2025年精彩三年就练这一本八年级数学上册浙教版》

1 在Rt△ABC中,∠C= 90°,AC= 9,BC= 12,则点C到AB的距离是( )

A.$\frac{36}{5}$
B.$\frac{12}{25}$
C.$\frac{9}{4}$
D.$\frac{27}{4}$

答案： A

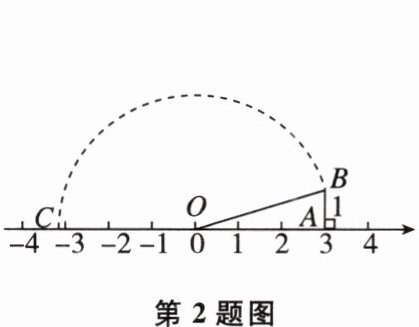
2 如图,数轴上点O,A所表示的数分别是0,3,过点A作AB⊥数轴,AB= 1,以O为圆心,OB长为半径画弧交数轴上A点的左侧一点C,则点C表示的数是( )

A.$\sqrt{10}$
B.$-\sqrt{10}$
C.$-\sqrt{8}$
D.$\sqrt{8}$

答案： B

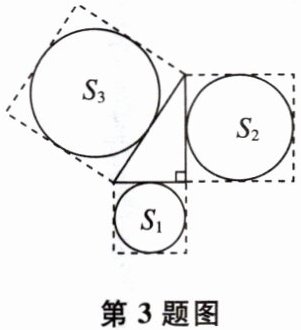
3 如图,分别以直角三角形的三边为边,向外作三个正方形,$S_1,S_2,S_3$是分别以直角三角形的三边长为直径的圆的面积。若$S_1= 36$,$S_2= 64$,则$S_3$的值为( )

A.$\frac{10\sqrt{\pi}}{\pi}$
B.10
C.100
D.$\frac{10}{\pi}$

答案： C

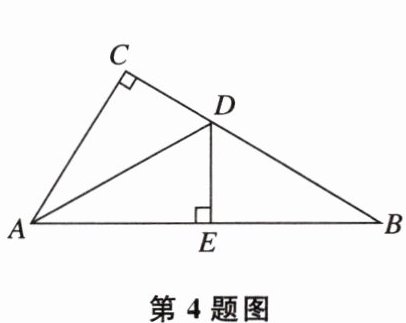
4 如图,在△ABC中,∠C= 90°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE= 1,BD= 2,若E是AB的中点,则AC的长为______。

答案： $\sqrt{3}$

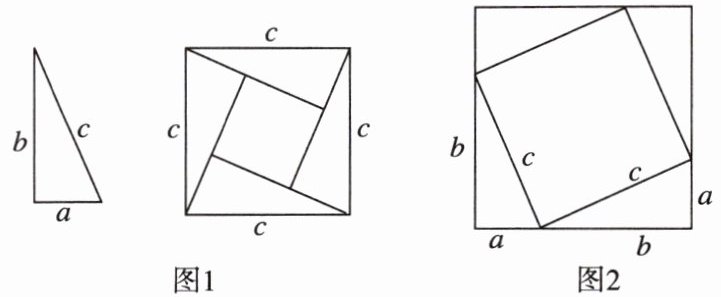
5 (1)我国著名的数学家赵爽,早在公元3世纪,就把一个长方形分成四个全等的直角三角形,用四个全等的直角三角形拼成了一个大的正方形(如图1),这个图形称为赵爽弦图,验证了一个非常重要的结论：在直角三角形中,两条直角边a,b与斜边c满足关系式$a^2+b^2= c^2$,称为勾股定理。
证明：因为大正方形的面积可表示为$S= c^2$,又可表示为$S= 4×\frac{1}{2}ab+(b-a)^2$,
所以$4×\frac{1}{2}ab+(b-a)^2= c^2$,
所以______,
即直角三角形两条直角边的平方和等于斜边的平方。
(2)爱动脑筋的小明把这四个全等的直角三角形拼成了另一个大的正方形(如图2),也能验证这个结论,请你帮助小明完成验证的过程。

答案： 解:
(1)$a^{2}+b^{2}=c^{2}$
(2)证明:由图得,大正方形面积$=\frac{1}{2}ab×4 + c^{2}=(a + b)^{2}$,
整理得,$2ab + c^{2}=a^{2}+b^{2}+2ab$,即$a^{2}+b^{2}=c^{2}$。