《2025年精彩三年就练这一本八年级数学上册浙教版》

1根据下列条件不能判断△ABC是直角三角形的是( )

A.∠A= 57.3°,∠B= 32°42'
B.∠B= ∠C= 45°
C.∠A= 2∠B= 3∠C
D.∠A∶∠B∶∠C= 17∶10∶7

答案： C

2在△ABC中,2∠A= ∠B= 60°,则△ABC是( )

A.锐角三角形
B.直角三角形
C.钝角三角形
D.锐角或钝角三角形

答案： B

3当三角形中的一个内角α是另一个内角β的一半时,我们称此三角形为“特征三角形”,其中α称为“特征角”。如果一个“特征三角形”为直角三角形,则这个“特征角”的度数为______。

答案： $45^{\circ}$或$30^{\circ}$

4如图,CE⊥AD,垂足为E,∠A= ∠C。求证：△ABD是直角三角形。

答案： 证明:因为 $CE\perp AD$,所以$\angle CED=90^{\circ}$,所以$\angle C+\angle D=90^{\circ}$。因为$\angle A=\angle C$,所以$\angle A+\angle D=90^{\circ}$,所以$\angle ABD=90^{\circ}$,所以$\triangle ABD$是直角三角形。

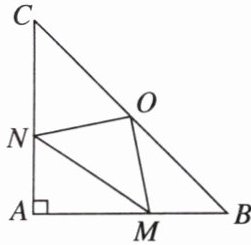
5如图,在△ABC中,∠A= 90°,AB= AC,O是BC的中点。如果在AB和AC上分别有一个动点M,N在移动,且在移动时始终保持AN= BM,请你判断△OMN的形状,并说明理由。

答案： 解:$\triangle OMN$是等腰直角三角形。理由:连结 OA(图略)。因为在$\triangle ABC$中,$\angle BAC=90^{\circ},AB=AC$,O 是 BC 的中点,所以 $AO=BO=CO,AO\perp BC,\angle CAO=\frac{1}{2}\angle BAC=45^{\circ},\angle B=\angle C=45^{\circ}$,所以$\angle NAO=\angle B$。在$\triangle OAN$和$\triangle OBM$中,因为$\left\{\begin{array}{l} AO=BO,\\ \angle NAO=\angle B,\\ AN=BM,\end{array}\right.$所以$\triangle OAN\cong\triangle OBM(SAS)$,所以 $ON=OM,\angle AON=\angle BOM$。又因为$\angle BOM+\angle AOM=90^{\circ}$,所以$\angle AON+\angle AOM=90^{\circ}$,即$\angle NOM=90^{\circ}$,所以$\triangle OMN$是等腰直角三角形。