《2025年精彩三年就练这一本八年级数学上册浙教版》

1 如图,∠A,∠1,∠2的大小关系是 ( )

A.∠A＞∠1＞∠2
B.∠2＞∠1＞∠A
C.∠A＞∠2＞∠1
D.∠2＞∠A＞∠1

答案： B

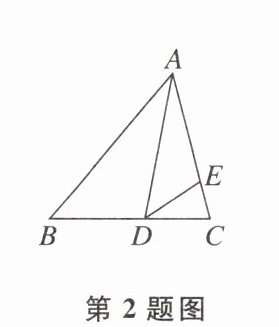
2 如图,在△ABC中,∠B= 50°,∠BAD= 28°,DE平分∠ADC,则∠EDC的度数是 ( )

A.78°
B.39°
C.25°
D.14°

答案： B

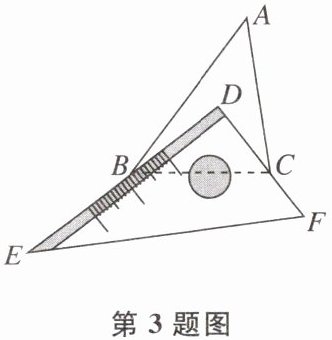
3 如图,有一块直角三角板DEF放置在△ABC上,三角板DEF的两条直角边DE,DF恰好分别经过点B,C。在△ABC中,∠DBA+∠DCA= 45°,则∠A的度数是 ( )

A.40°
B.44°
C.45°
D.50°

答案： C

4 如图,在△ABC中,∠ABC,∠ACB的平分线BO,CO交于点O,CE为△ABC的外角∠ACD的平分线,BO的延长线交CE于点E,∠1= α,则∠2的大小为 。(用含α的式子表示)

答案： $\frac{1}{2}\alpha$【解析】因为$\angle ABC,\angle ACB$的平分线 BO,CO 交于点O,所以$\angle CBE=\frac{1}{2}\angle ABC$。
因为 CE 为$\triangle ABC$的外角$\angle ACD$的平分线，所以$\angle ACE=\angle DCE=\frac{1}{2}\angle ACD$。
因为$\angle ACD=180^{\circ }-\angle ACB=180^{\circ }-(180^{\circ }-\angle ABC-\angle 1)=\angle 1+\angle ABC$，$\angle ECD=180^{\circ }-\angle ECB=180^{\circ }-(180^{\circ }-\angle EBC-\angle 2)=\angle EBC+\angle 2$，
所以$\angle 2=\angle ECD-\angle EBC=\frac{1}{2}(\angle ACD-\angle ABC)=\frac{1}{2}\angle 1=\frac{1}{2}\alpha$。

5 如图,△ABC的外角∠ACD的平分线与线段BA的延长线交于点F,点E在线段CF上,且∠AEF+∠FCD= 180°。
(1)求证：AE//BC。
(2)若∠B= 28°,∠ACF= 62°,求∠BAC的度数。

答案： 解:
(1)证明:因为$\angle AEF+\angle AEC=180^{\circ }$，$\angle AEF+\angle FCD=180^{\circ }$，
所以$\angle AEC=\angle FCD$，
所以$AE// BC$。
(2)因为 CF 是$\angle ACD$的平分线，$\angle ACF=62^{\circ }$，
所以$\angle ACD=2\angle ACF=124^{\circ }$。
因为$\angle B=28^{\circ }$，
所以$\angle BAC=\angle ACD-\angle B=124^{\circ }-28^{\circ }=96^{\circ }$。