《2025年精彩三年就练这一本八年级数学上册浙教版》

1如图,∠A= ∠D= 90°,AC= DB,则△ABC≌△DCB的依据是 ( )

A.HL
B.ASA
C.AAS
D.SAS

答案： A

2如图,已知AB⊥BD,CD⊥BD,若用“HL”判定Rt△ABD和Rt△CDB全等,则需要添加的条件是 ( )

A.∠A= ∠C
B.∠CBD= ∠ADB
C.AB= CD
D.AD= CB

答案： D

3下列说法正确的是 ( )

A.面积相等的两个三角形全等
B.形状相同的两个三角形全等
C.三个角分别相等的两个三角形全等
D.斜边和一条直角边对应相等的两个直角三角形全等

答案： D

4小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线。如图,一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说：“射线OP就是∠BOA的平分线。”小明的做法,其理论依据是______。

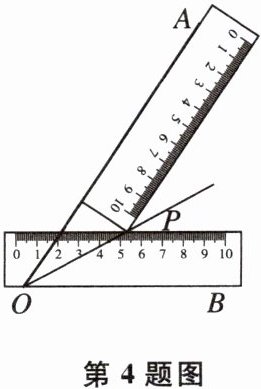
答案： 角的内部，到角两边距离相等的点，在这个角的平分线上

5数学兴趣小组在解决一道数学题：如图,AC⊥BC,BD⊥AD,AD= BC。求证：BD= AC。
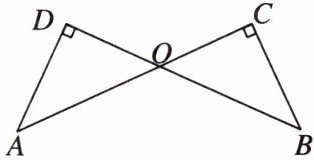
小丽说：“我可以根据全等三角形的判定定理‘AAS’证明两个三角形全等,从而得到BD= AC。”
小贾说：“我可以根据直角三角形全等的判定定理‘HL’证明两个三角形全等,从而得到BD= AC。”
小雨说：“我可以根据三角形的面积相等,来证明BD= AC。”
你认为他们的办法可行吗？并试着证明。

答案：
解：都可行。
证明1：因为AC⊥BC，BD⊥AD，
所以∠D=∠C=90°。
在△AOD和△BOC中，
∠D=∠C，
∠AOD=∠BOC，
AD=BC，
所以△AOD≌△BOC(AAS)，
所以AO=BO，DO=CO，
所以AO+CO=BO+DO，即BD=AC。故小丽的办法可行。
证明2：连结AB，如图。
因为AC⊥BC，BD⊥AD，
所以∠D=∠C=90°。
在Rt△ABD和Rt△BAC中，
AD=BC，
AB=BA，
所以Rt△ABD≌Rt△BAC(HL)，
所以BD=AC。故小贾的办法可行。

证明3：连结AB，由证明1得知△AOD≌△BOC，
所以S△AOD=S△BOC，
所以S△AOD+S△AOB=S△BOC+S△AOB，即S△ABD=S△ABC，
又因为S△ABD= $\frac{1}{2}$AD·BD，S△ABC= $\frac{1}{2}$BC·AC，
所以$\frac{1}{2}$AD·BD= $\frac{1}{2}$BC·AC。
因为AD=BC，
所以BD=AC。故小雨的办法可行。