《2025年精彩三年就练这一本八年级数学上册浙教版》

❶如图，在$\triangle ABC$中，边$AB$上的高是（ ）

A.$AF$
B.$BE$
C.$CE$
D.$BD$

答案： C

❷在$\triangle ABC$中，线段$AP$，$AQ$，$AR$分别是$BC$边上的高线、中线和角平分线，则（ ）

A.$AP\leqslant AQ$
B.$AQ\leqslant AR$
C.$AP＞AR$
D.$AP＞AQ$

答案： A

❸已知$\triangle ABC$的高线$AD$在$\triangle ABC$的外部，则$\angle A$的取值范围是________。

答案： $0^{\circ}＜\angle A＜90^{\circ}$

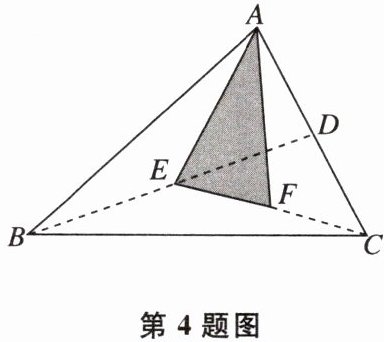
❹如图，在$\triangle ABC$中，已知$D$，$E$，$F$分别为边$AC$，$BD$，$CE$的中点，且阴影部分的面积等于$4\ cm^2$，则$\triangle ABC$的面积为______$cm^2$。

答案： 16

❺(1)如图1，在$\triangle ABC$中，$AD$，$AE$分别是$\triangle ABC$的高线和角平分线，已知$\angle B=30^\circ$，$\angle C=50^\circ$。求$\angle DAE$的度数。

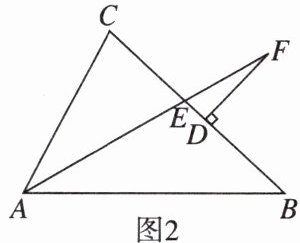
(2)如图2，$\angle BAC$的平分线$AF$交$BC$于点$E$，过点$F$作$FD\perp BC$于点$D$，若$\angle B=x^\circ$，$\angle C=(x+30)^\circ$。
①$\angle CAE=$______。（用含$x$的代数式表示）
②求$\angle F$的度数。

答案： 解:
(1)因为$\angle B=30^{\circ}$,$\angle C=50^{\circ}$,所以$\angle CAB=180^{\circ}-\angle B-\angle C=100^{\circ}$。因为 AE 是$\triangle ABC$的角平分线，所以$\angle CAE=\frac{1}{2}\angle CAB=50^{\circ}$。因为 AD 是$\triangle ABC$的高线，所以$\angle ADC=90^{\circ}$,所以$\angle CAD=90^{\circ}-\angle C=40^{\circ}$,所以$\angle DAE=\angle CAE-\angle CAD=50^{\circ}-40^{\circ}=10^{\circ}$。
(2)①$(75-x)^{\circ}$②因为$\angle AEC=180^{\circ}-\angle C-\angle EAC=75^{\circ}$,所以$\angle FED=75^{\circ}$。因为$FD\perp BC$,所以$\angle F=15^{\circ}$。