《2025年精彩三年就练这一本八年级数学上册浙教版》

1 某函数图象如图所示,那么函数中( )

A.$ y $ 随 $ x $ 增大而增大
B.$ y $ 随 $ x $ 增大而减小
C.$ y $ 随 $ x $ 有时增大有时减小
D.$ x $ 增大时 $ y $ 保持不变

答案： B

2 如图,一个函数的图象由射线 $ BA $、线段 $ BC $、射线 $ CD $ 组成,其中点 $ A(-1,2) $,$ B(1,3) $,$ C(2,1) $,$ D(6,5) $,则此函数在 $ -1 \leq x \leq 6 $ 时的最小值是( )

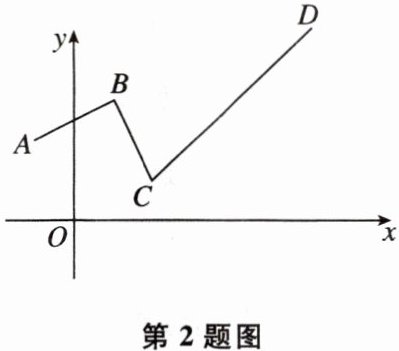
A.$ -1 $
B.$ 1 $
C.$ 2 $
D.$ 3 $

答案： B

3 如图,这是一个高为 24 的容器,现向容器匀速注水,下列图象中能大致反映容器中水的深度 $ (h) $ 与注水量 $ (V) $ 关系的是( )

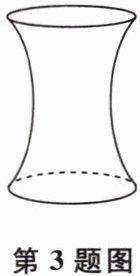
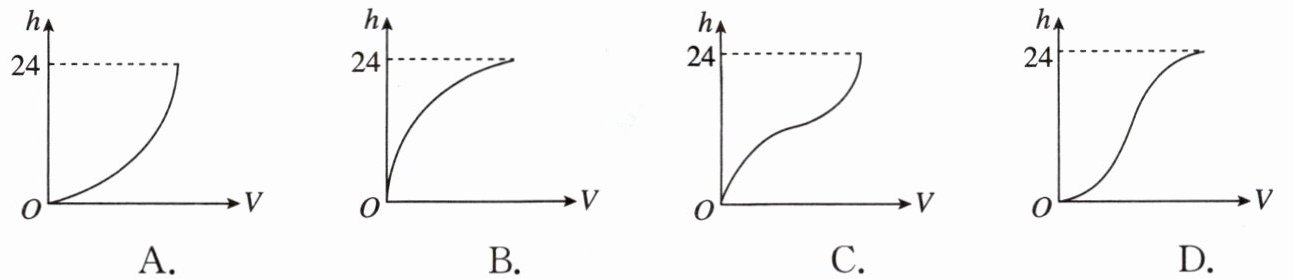
答案： D

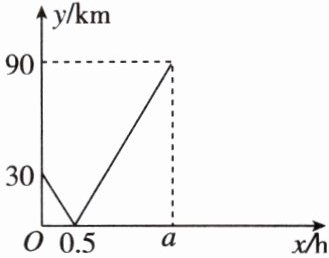
4 在一条笔直的航道上依次有甲、乙、丙三个港口,一艘船从甲港出发,沿直线匀速行驶经过乙港驶向丙港,最终到达丙港,设行驶 $ x(h) $ 后,与乙港的距离为 $ y(km) $,$ y $ 与 $ x $ 的关系如图所示,下列结论：
①甲港与丙港的距离是 90 km；
②船在中途休息了 0.5 h；
③船的行驶速度是 45 km/h；
④ $ a $ 的值为 2。
其中正确的是______。(只填序号)

答案： ④

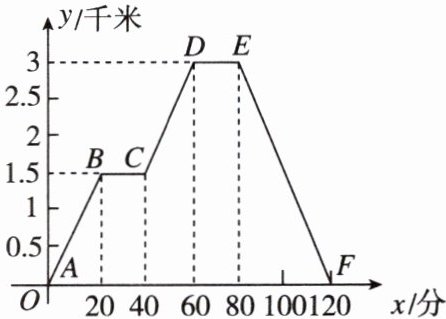
5 小明从大明宫丹凤门出发。沿公园游览步道步行参观大明宫国家遗址公园,已知他离丹凤门的距离 $ y $(千米)与出发时间 $ x $(分)之间的关系如图所示。请根据图象回答下列问题：
(1)图象中的 $ C $ 点表示什么？
(2)小明游览过程中离丹凤门的最远距离是______千米,小明在游览过程中共休息了______分钟。
(3)计算小明在 $ CD $ 路段内的步行速度是多少千米/时。

答案： 解:
(1)图象中的 C 点表示小明在游览过程中第一次休息了20 分钟后继续前行。
(2)由图象知,小明在游览过程中离丹风门的最远距离是3 千米；小明在游览过程中共休息了(40-20)+(80-60)=40(分);故答案为 3;40。
(3)小明在 CD 路段步行的路程为 3-1.5=1.5(千米),所用的时间为 $\frac{60-40}{60}=\frac{1}{3}$(小时),故小明在 CD 路段内步行的速度是 $1.5÷\frac{1}{3}=4.5$(千米/时)。