第89页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
23 如图,在矩形 $ABCD$ 中,$AB = 6$,$BC = 8$,点 $E$ 是 $BC$ 边上一点,连接 $AE$,把 $\angle B$ 沿 $AE$ 折叠,使点 $B$ 落在点 $B'$ 处,当 $\triangle CEB'$ 为直角三角形时,求 $BE$ 的长度。
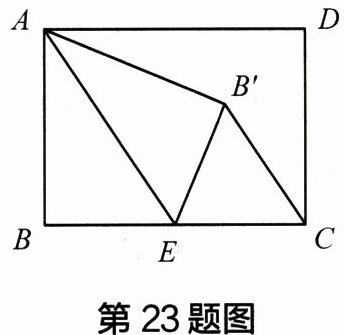

答案:
①当∠CB'E=90°,即点B'在AC上时,此时BE=3;②当∠CEB'=90°时,点B'在AD上,此时BE=6。
24 探究一:如图①,$P$、$Q$、$M$ 均为正方形。
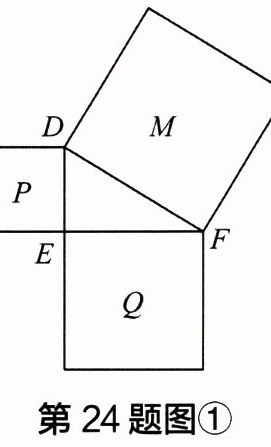
问题:(1)若图①中的 $\triangle DEF$ 为直角三角形,$P$ 的面积为 $3$,$Q$ 的面积为 $10$,则 $M$ 的面积为______;
(2)若 $P$ 的面积为 $15cm^2$,$Q$ 的面积为 $45cm^2$,同时 $M$ 的面积为 $60cm^2$,则 $\triangle DEF$ 为______三角形。
探究二:图形变化:
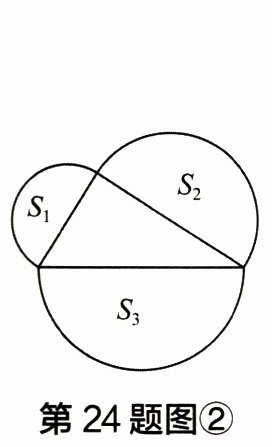
(3)如图②,分别以直角三角形的三边为直径向三角形外作三个半圆,判断这三个半圆的面积之间有什么关系,并说说你的理由;
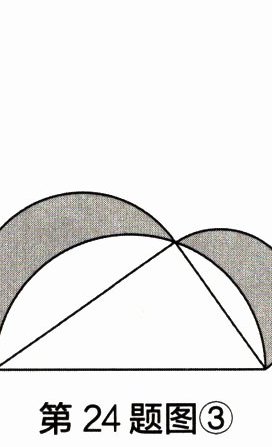
(4)如图③,如果直角三角形两直角边长分别为 $6$ 和 $8$,以直角三角形的三边为直径作半圆,你能利用上面的结论求出阴影部分的面积吗?如果能,请写出你的计算过程;如果不能,请说明理由。



问题:(1)若图①中的 $\triangle DEF$ 为直角三角形,$P$ 的面积为 $3$,$Q$ 的面积为 $10$,则 $M$ 的面积为______;
(2)若 $P$ 的面积为 $15cm^2$,$Q$ 的面积为 $45cm^2$,同时 $M$ 的面积为 $60cm^2$,则 $\triangle DEF$ 为______三角形。
探究二:图形变化:
(3)如图②,分别以直角三角形的三边为直径向三角形外作三个半圆,判断这三个半圆的面积之间有什么关系,并说说你的理由;
(4)如图③,如果直角三角形两直角边长分别为 $6$ 和 $8$,以直角三角形的三边为直径作半圆,你能利用上面的结论求出阴影部分的面积吗?如果能,请写出你的计算过程;如果不能,请说明理由。
答案:
探究一:
(1)13
(2)直角探究二:
(3)S₁+S₂=S₃。理由如下:设直角三角形的三边分别为a、b、c(a<b<c),则a²+b²=c²。S₁=1/2×(a/2)²×π=a²π/8,S₂=1/2×(b/2)²×π=b²π/8,S₃=1/2×(c/2)²×π=c²π/8,因为S₁+S₂=a²π/8+b²π/8=(a²+b²)×π/8=c²π/8,所以S₁+S₂=S₃。
(4)由图②可知S阴影=S直角三角形=1/2×6×8=24。
(1)13
(2)直角探究二:
(3)S₁+S₂=S₃。理由如下:设直角三角形的三边分别为a、b、c(a<b<c),则a²+b²=c²。S₁=1/2×(a/2)²×π=a²π/8,S₂=1/2×(b/2)²×π=b²π/8,S₃=1/2×(c/2)²×π=c²π/8,因为S₁+S₂=a²π/8+b²π/8=(a²+b²)×π/8=c²π/8,所以S₁+S₂=S₃。
(4)由图②可知S阴影=S直角三角形=1/2×6×8=24。
查看更多完整答案,请扫码查看


