第76页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
23 我们知道在解与角平分线有关的问题时,通常过角平分线上的一点作角两边的垂线,构造全等三角形,请完成下列问题。
【初步探究】
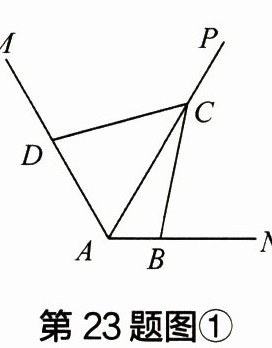
(1) 如图①,$ \angle MAN = 120^{\circ} $,$ AP $ 平分 $ \angle MAN $,点 $ C $ 是射线 $ AP $ 上一点,$ \angle BCD = 60^{\circ} $,且与 $ AM $、$ AN $ 分别交于点 $ D $、$ B $,求证:$ CD = CB $;
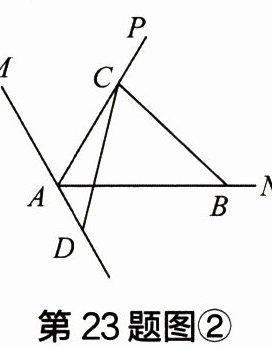
【类比探究】(2) 如图②,其他条件不变,将图①的 $ \angle BCD $ 绕点 $ C $ 逆时针旋转使点 $ D $ 落在 $ AM $ 的反向延长线上。请探究线段 $ AB $、$ AC $ 和 $ AD $ 之间的数量关系,写出结论并证明;
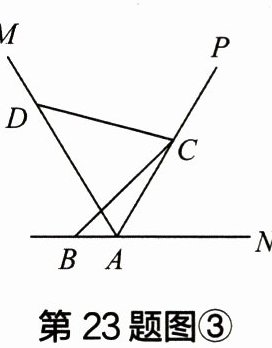
【拓展应用】(3) 如图③,其他条件不变,将图①的 $ \angle BCD $ 绕点 $ C $ 顺时针旋转使点 $ B $ 落在 $ AN $ 的反向延长线上。请直接写出线段 $ AB $、$ AC $ 和 $ AD $ 之间的数量关系。(不用证明)



【初步探究】
(1) 如图①,$ \angle MAN = 120^{\circ} $,$ AP $ 平分 $ \angle MAN $,点 $ C $ 是射线 $ AP $ 上一点,$ \angle BCD = 60^{\circ} $,且与 $ AM $、$ AN $ 分别交于点 $ D $、$ B $,求证:$ CD = CB $;
【类比探究】(2) 如图②,其他条件不变,将图①的 $ \angle BCD $ 绕点 $ C $ 逆时针旋转使点 $ D $ 落在 $ AM $ 的反向延长线上。请探究线段 $ AB $、$ AC $ 和 $ AD $ 之间的数量关系,写出结论并证明;
【拓展应用】(3) 如图③,其他条件不变,将图①的 $ \angle BCD $ 绕点 $ C $ 顺时针旋转使点 $ B $ 落在 $ AN $ 的反向延长线上。请直接写出线段 $ AB $、$ AC $ 和 $ AD $ 之间的数量关系。(不用证明)
答案:
(1)如图①,过点 C 作 CE⊥AN 于点 E,过点 C 作 CF⊥AM 于点 F,所以∠CFD=∠CEA=90°。因为 AC 是∠MAN 的平分线,所以 CE=CF。因为∠MAN=120°,所以∠ECF=360° - 90° - 90° - 120°=60°。因为∠BCD=60°,所以∠DCF=60° - ∠BCF,∠BCE=60° - ∠BCF,所以∠DCF=∠BCE,所以△CDF≌△CBE(AAS),所以 CD=CB。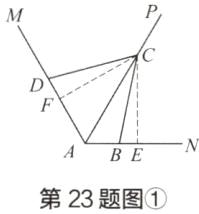
(2)AB=AC+AD。理由如下:如图②,在 AB 上截取 AG=AC,连接 CG。因为∠PAB=$\frac{1}{2}$∠MAN=60°,所以△ACG 是等边三角形,所以 AC=CG=AG。由
(1)知,BC=CD,∠BCD=60°,因为∠ACG=∠ACD+∠DCG=60°,∠BCD=∠DCG+∠BCG=60°,所以∠ACD=∠BCG,因为∠MAN=120°,∠AGC=60°,所以∠CAD=∠CGB=120°,所以△BCG≌△DCA(AAS),所以 AD=BG,所以 AB=AG+BG=AC+AD。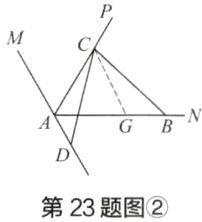
(3)AD=AB+AC。理由如下:如图③,在 AD 上截取 AH=AC,连接 CH。因为∠MAC=60°,所以△ACH 是等边三角形,所以 AH=CH=AC。因为∠CHA=60°,∠MAC=∠CAN=60°,所以∠CHD=∠BAC=120°。因为∠ACH=∠BCA+∠HCB=60°,∠DCB=∠DCH+∠BCH=60°,所以∠DCH=∠BCA,所以△CDH≌△CBA(AAS),所以 DH=AB,所以 AD=DH+AH=AB+AC,即 AD=AB+AC。
(1)如图①,过点 C 作 CE⊥AN 于点 E,过点 C 作 CF⊥AM 于点 F,所以∠CFD=∠CEA=90°。因为 AC 是∠MAN 的平分线,所以 CE=CF。因为∠MAN=120°,所以∠ECF=360° - 90° - 90° - 120°=60°。因为∠BCD=60°,所以∠DCF=60° - ∠BCF,∠BCE=60° - ∠BCF,所以∠DCF=∠BCE,所以△CDF≌△CBE(AAS),所以 CD=CB。

(2)AB=AC+AD。理由如下:如图②,在 AB 上截取 AG=AC,连接 CG。因为∠PAB=$\frac{1}{2}$∠MAN=60°,所以△ACG 是等边三角形,所以 AC=CG=AG。由
(1)知,BC=CD,∠BCD=60°,因为∠ACG=∠ACD+∠DCG=60°,∠BCD=∠DCG+∠BCG=60°,所以∠ACD=∠BCG,因为∠MAN=120°,∠AGC=60°,所以∠CAD=∠CGB=120°,所以△BCG≌△DCA(AAS),所以 AD=BG,所以 AB=AG+BG=AC+AD。

(3)AD=AB+AC。理由如下:如图③,在 AD 上截取 AH=AC,连接 CH。因为∠MAC=60°,所以△ACH 是等边三角形,所以 AH=CH=AC。因为∠CHA=60°,∠MAC=∠CAN=60°,所以∠CHD=∠BAC=120°。因为∠ACH=∠BCA+∠HCB=60°,∠DCB=∠DCH+∠BCH=60°,所以∠DCH=∠BCA,所以△CDH≌△CBA(AAS),所以 DH=AB,所以 AD=DH+AH=AB+AC,即 AD=AB+AC。

查看更多完整答案,请扫码查看


