第18页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
20 (1)计算:$ | 1 - \sqrt { 5 } | + \sqrt { ( - 5 ) ^ { 2 } } + ( \sqrt { 10 } - \pi ) ^ { 0 } $;
(2)已知 $ 3 ( x - 1 ) ^ { 2 } - 75 = 0 $,求 $ x $ 的值。
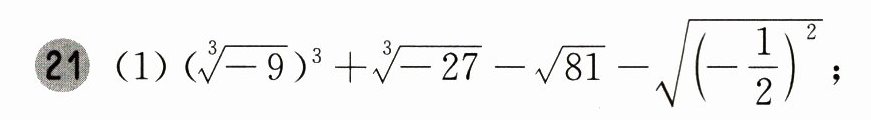
(2)已知 $ 3 ( x - 1 ) ^ { 2 } - 75 = 0 $,求 $ x $ 的值。
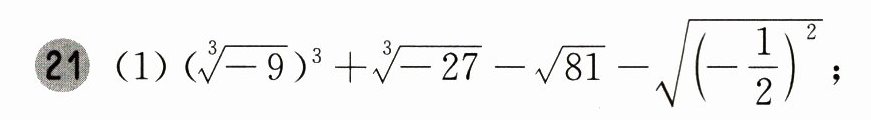
答案:
(1)√5+5;
(2)x=6或-4
(1)√5+5;
(2)x=6或-4
(2)已知 $ 2 x + 1 $ 的算术平方根是 3,$ 2 x + y - 4 $ 的立方根是 -2,求 $ x - y $ 的平方根。
答案:
x - y的平方根为±4
22 光年是距离单位,1 光年 $ \approx 9.46 × 10 ^ { 12 } $ 千米,人类所观测的宇宙深度已达到 150 亿光年。纳米是表示微小距离的单位,1 米 $ = 10 ^ { 9 } $ 纳米。纳米材料学作为一门新兴学科正成为跨世纪的科技热点之一。请回答下列问题:(用科学记数法表示)
(1)你知道 1 千米是多少纳米吗?
(2)你知道 1 光年约是多少纳米吗?
(3)人类所观测到的宇宙深度约为多少米?
(1)你知道 1 千米是多少纳米吗?
(2)你知道 1 光年约是多少纳米吗?
(3)人类所观测到的宇宙深度约为多少米?
答案:
(1)10¹²(纳米)
(2)9.46×10²⁴(纳米)
(3)1.419×10²⁶(米)
(1)10¹²(纳米)
(2)9.46×10²⁴(纳米)
(3)1.419×10²⁶(米)
23 我们知道:任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零。由此可得:如果 $ a x + b = 0 $,其中 $ a $、$ b $ 为有理数,$ x $ 为无理数,那么 $ a = 0 $ 且 $ b = 0 $。运用上述知识,解决下列问题:
(1)如果 $ ( a + 2 ) \sqrt { 2 } - b + 3 = 0 $,其中 $ a $、$ b $ 为有理数,那么 $ a = $______,$ b = $______;
(2)如果 $ 2 b - a - ( a + b - 4 ) \sqrt { 3 } = 5 $,其中 $ a $、$ b $ 为有理数,求 $ 3 a + 2 b $ 的平方根。
(1)如果 $ ( a + 2 ) \sqrt { 2 } - b + 3 = 0 $,其中 $ a $、$ b $ 为有理数,那么 $ a = $______,$ b = $______;
(2)如果 $ 2 b - a - ( a + b - 4 ) \sqrt { 3 } = 5 $,其中 $ a $、$ b $ 为有理数,求 $ 3 a + 2 b $ 的平方根。
答案:
(1)-2,3
(2)±3
(1)-2,3
(2)±3
查看更多完整答案,请扫码查看


