第84页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
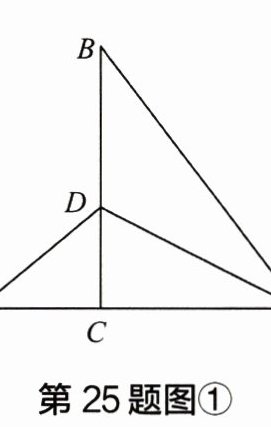
25 如图①,$Rt\triangle ABC$中,$\angle ACB= 90^{\circ}$,$AC= 6$,$BC= 8$,点$D在BC$边上,将$\triangle ABD沿直线AD$翻折,点$B的对应点B'恰好落在AC$的延长线上,连接$B'D$。
(1) 求$CD$的长。
(2) 如图②,点$E在线段AD$上,连接$BE$、$EB'$、$BB'$,当$\triangle EBB'$是等腰直角三角形时:
① 求证:点$E在\angle ACB$的平分线上;
② 求点$E到AC$的距离。
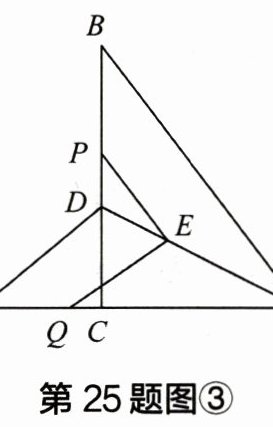
(3) 如图③,在(2)的条件下,点$P从点B$出发以每秒 2 个单位长度的速度沿$BC往点C$运动,连$PE$,过点$E作EP$的垂线,交直线$AC于点Q$,问点$P$运动多少秒时,$\triangle AEQ$是等腰三角形?


(1) 求$CD$的长。
(2) 如图②,点$E在线段AD$上,连接$BE$、$EB'$、$BB'$,当$\triangle EBB'$是等腰直角三角形时:
① 求证:点$E在\angle ACB$的平分线上;
② 求点$E到AC$的距离。
(3) 如图③,在(2)的条件下,点$P从点B$出发以每秒 2 个单位长度的速度沿$BC往点C$运动,连$PE$,过点$E作EP$的垂线,交直线$AC于点Q$,问点$P$运动多少秒时,$\triangle AEQ$是等腰三角形?




答案:
(1)由翻折可得AD为∠BAC的平分线,如图①,作DE⊥AB于点E,则DE=DC,在Rt△ABC中,由勾股定理得$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{6^{2}+8^{2}}=10$,因为$S_{\triangle ABD}=\frac{1}{2}AB\cdot DE$,$S_{\triangle ACD}=\frac{1}{2}AC\cdot CD$,所以$\frac{S_{\triangle ABD}}{S_{\triangle ACD}}=\frac{\frac{1}{2}AB\cdot DE}{\frac{1}{2}AC\cdot CD}=\frac{AB}{AC}=\frac{10}{6}=\frac{5}{3}$。又因为$\frac{S_{\triangle ABD}}{S_{\triangle ACD}}=\frac{BD}{CD}$),所以$\frac{BD}{CD}=\frac{5}{3}$,所以$CD=\frac{3}{8}BC=\frac{3}{8}×8=3$。
(2)①证明:如图②,过点E作EN⊥BC于点N,EM⊥AC于点M,设B'E交BC于点K。因为∠B'KC=∠BKE,且∠BEK=∠B'CK=90°,所以∠NBE=∠EB'M。因为B'E=BE,∠BNE=∠B'ME=90°,所以△BEN≌△B'EM(AAS),所以EM=EN。因为EN⊥BC,EM⊥AC,所以E在∠ACB的角平分线上;
②因为EN⊥BC,EM⊥AC,∠MCN=90°,所以四边形EMCN为矩形,因为EM=EN,所以矩形EMCN为正方形,设EN=a,则ME=EN=CM=CN=a。因为△BEN≌△B'EM,所以BN=B'M,所以BC - CN=B'C+CM,即8 - a=a + 4,解得a=2,即EM=2。所以E到AC的距离为2。
(3)由
(2)可知E在∠ACB的角平分线上,如图③,作EM⊥BC于点M,EN⊥AC于点N,所以EM=EN=2。由
(2)可知,四边形EMCN是正方形,所以∠MEN=90°=∠PEQ,所以∠PEM=∠QEN。因为∠PME=∠QNE=90°,EM=EN,所以△PME≌△QNE(ASA),所以PM=QN。当AE=EQ时,因为EN⊥AQ,所以AN=QN=AC - CN=4,所以PM=QN=4,所以CP=CM+PM=6,所以BP=8 - 6=2,所以$t=\frac{2}{2}=1$;当AE=AQ时,$AE=\sqrt{EN^{2}+AN^{2}}=\sqrt{2^{2}+4^{2}}=2\sqrt{5}$,所以$AQ=AE=2\sqrt{5}$,因为AN=4,所以$QN=2\sqrt{5}-4=PM$,所以$CP=CM+PM=2+2\sqrt{5}-4=2\sqrt{5}-2$,所以$BP=BC - CP=8-(2\sqrt{5}-2)=10 - 2\sqrt{5}$,所以$t=\frac{10 - 2\sqrt{5}}{2}=5-\sqrt{5}$;当$EQ = QA$时,设$QN = b$,则$AQ = 4 - b = EQ$,因为∠ENQ = 90°,所以$EQ^{2}=EN^{2}+NQ^{2}$,即$(4 - b)^{2}=b^{2}+2^{2}$,解得$b=\frac{3}{2}$。所以$QN=\frac{3}{2}=PM$,所以$CP=2-\frac{3}{2}=\frac{1}{2}$,所以$BP=BC - CP=8-\frac{1}{2}=\frac{15}{2}$,所以$t=\frac{\frac{15}{2}}{2}=\frac{15}{4}$。综上所述,当P的运动时间为1秒或$(5-\sqrt{5})$秒或$\frac{15}{4}$秒时,△AEQ是等腰三角形。
(1)由翻折可得AD为∠BAC的平分线,如图①,作DE⊥AB于点E,则DE=DC,在Rt△ABC中,由勾股定理得$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{6^{2}+8^{2}}=10$,因为$S_{\triangle ABD}=\frac{1}{2}AB\cdot DE$,$S_{\triangle ACD}=\frac{1}{2}AC\cdot CD$,所以$\frac{S_{\triangle ABD}}{S_{\triangle ACD}}=\frac{\frac{1}{2}AB\cdot DE}{\frac{1}{2}AC\cdot CD}=\frac{AB}{AC}=\frac{10}{6}=\frac{5}{3}$。又因为$\frac{S_{\triangle ABD}}{S_{\triangle ACD}}=\frac{BD}{CD}$),所以$\frac{BD}{CD}=\frac{5}{3}$,所以$CD=\frac{3}{8}BC=\frac{3}{8}×8=3$。
(2)①证明:如图②,过点E作EN⊥BC于点N,EM⊥AC于点M,设B'E交BC于点K。因为∠B'KC=∠BKE,且∠BEK=∠B'CK=90°,所以∠NBE=∠EB'M。因为B'E=BE,∠BNE=∠B'ME=90°,所以△BEN≌△B'EM(AAS),所以EM=EN。因为EN⊥BC,EM⊥AC,所以E在∠ACB的角平分线上;
②因为EN⊥BC,EM⊥AC,∠MCN=90°,所以四边形EMCN为矩形,因为EM=EN,所以矩形EMCN为正方形,设EN=a,则ME=EN=CM=CN=a。因为△BEN≌△B'EM,所以BN=B'M,所以BC - CN=B'C+CM,即8 - a=a + 4,解得a=2,即EM=2。所以E到AC的距离为2。
(3)由
(2)可知E在∠ACB的角平分线上,如图③,作EM⊥BC于点M,EN⊥AC于点N,所以EM=EN=2。由
(2)可知,四边形EMCN是正方形,所以∠MEN=90°=∠PEQ,所以∠PEM=∠QEN。因为∠PME=∠QNE=90°,EM=EN,所以△PME≌△QNE(ASA),所以PM=QN。当AE=EQ时,因为EN⊥AQ,所以AN=QN=AC - CN=4,所以PM=QN=4,所以CP=CM+PM=6,所以BP=8 - 6=2,所以$t=\frac{2}{2}=1$;当AE=AQ时,$AE=\sqrt{EN^{2}+AN^{2}}=\sqrt{2^{2}+4^{2}}=2\sqrt{5}$,所以$AQ=AE=2\sqrt{5}$,因为AN=4,所以$QN=2\sqrt{5}-4=PM$,所以$CP=CM+PM=2+2\sqrt{5}-4=2\sqrt{5}-2$,所以$BP=BC - CP=8-(2\sqrt{5}-2)=10 - 2\sqrt{5}$,所以$t=\frac{10 - 2\sqrt{5}}{2}=5-\sqrt{5}$;当$EQ = QA$时,设$QN = b$,则$AQ = 4 - b = EQ$,因为∠ENQ = 90°,所以$EQ^{2}=EN^{2}+NQ^{2}$,即$(4 - b)^{2}=b^{2}+2^{2}$,解得$b=\frac{3}{2}$。所以$QN=\frac{3}{2}=PM$,所以$CP=2-\frac{3}{2}=\frac{1}{2}$,所以$BP=BC - CP=8-\frac{1}{2}=\frac{15}{2}$,所以$t=\frac{\frac{15}{2}}{2}=\frac{15}{4}$。综上所述,当P的运动时间为1秒或$(5-\sqrt{5})$秒或$\frac{15}{4}$秒时,△AEQ是等腰三角形。
查看更多完整答案,请扫码查看


