2025年暑假衔接八年级数学浙教版延边人民出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假衔接八年级数学浙教版延边人民出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第8页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
17. 已知DH是BC边的垂直平分线,AD是$△ABC$的外角$∠BAG$的平分线,两线交于点D,$DF⊥AB$,垂足为F,$DE⊥CG$,垂足为E.
(1)求证:$BF=CE$.
(2)若$AC=4cm,AB=8cm$,求AE的长.
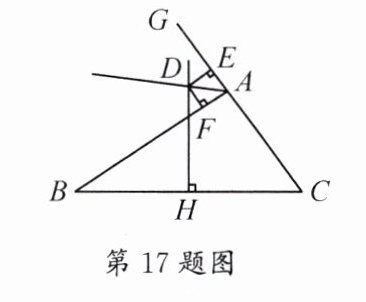
(1)证明:连结 BD,CD. ∵DH 是 BC 边的垂直平分线,$\therefore DB=DC$; ∵DA 平分$∠BAG,DE⊥CG,DF⊥AB,\therefore DE=DF,∠DEC=∠DFB=90^{\circ },\therefore Rt△DEC≌Rt△DFB(HL),\therefore BF=CE$.
(2)$\because AD=AD,DE=DF,∠DEA=∠DFA=90^{\circ },\therefore Rt△DEA≌Rt△DFA(HL),\therefore AE=AF,\therefore AE=AF=AB - BF=AB - CE=AB - AC - AE,\therefore 2AE=AB - AC=8 - 4=4(cm),\therefore AE=$
(1)求证:$BF=CE$.
(2)若$AC=4cm,AB=8cm$,求AE的长.

(1)证明:连结 BD,CD. ∵DH 是 BC 边的垂直平分线,$\therefore DB=DC$; ∵DA 平分$∠BAG,DE⊥CG,DF⊥AB,\therefore DE=DF,∠DEC=∠DFB=90^{\circ },\therefore Rt△DEC≌Rt△DFB(HL),\therefore BF=CE$.
(2)$\because AD=AD,DE=DF,∠DEA=∠DFA=90^{\circ },\therefore Rt△DEA≌Rt△DFA(HL),\therefore AE=AF,\therefore AE=AF=AB - BF=AB - CE=AB - AC - AE,\therefore 2AE=AB - AC=8 - 4=4(cm),\therefore AE=$
2cm
答案:
(1)证明:连结 BD,CD.
∵DH 是 BC 边的垂直平分线,$\therefore DB=DC$;
∵DA 平分$∠BAG,DE⊥CG,DF⊥AB,\therefore DE=DF,∠DEC=∠DFB=90^{\circ },\therefore Rt△DEC≌Rt△DFB(HL),\therefore BF=CE$.
(2)$\because AD=AD,DE=DF,∠DEA=∠DFA=90^{\circ },\therefore Rt△DEA≌Rt△DFA(HL),\therefore AE=AF,\therefore AE=AF=AB - BF=AB - CE=AB - AC - AE,\therefore 2AE=AB - AC=8 - 4=4(cm),\therefore AE=2cm$
(1)证明:连结 BD,CD.
∵DH 是 BC 边的垂直平分线,$\therefore DB=DC$;
∵DA 平分$∠BAG,DE⊥CG,DF⊥AB,\therefore DE=DF,∠DEC=∠DFB=90^{\circ },\therefore Rt△DEC≌Rt△DFB(HL),\therefore BF=CE$.
(2)$\because AD=AD,DE=DF,∠DEA=∠DFA=90^{\circ },\therefore Rt△DEA≌Rt△DFA(HL),\therefore AE=AF,\therefore AE=AF=AB - BF=AB - CE=AB - AC - AE,\therefore 2AE=AB - AC=8 - 4=4(cm),\therefore AE=2cm$
18. 折纸是我国一项古老的传统民间艺术,这项具有中国特色的传统文化在几何中可以得到新的解读. 请根据题意,探索不同情境中$∠1+∠2$(或$∠1-∠2$)与$∠A$的数量关系.
(1)如图1,已知在$△ABC$中,$∠A=60^{\circ }$,若沿图中虚线DE截去$∠A$,则$∠1+∠2=$______.
(2)如图2,翻折后,点A落在点$A'$处,若$∠1+∠2=110^{\circ }$,求$∠B+∠C$的度数.
(3)如图3,将$△ABC$沿DE折叠,使点A落在点$A'$处,若$∠1=80^{\circ },∠2=28^{\circ }$,则$∠A$的度数为______.
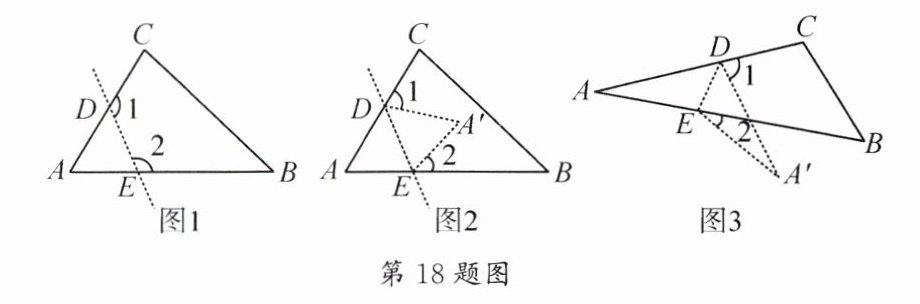
(1)如图1,已知在$△ABC$中,$∠A=60^{\circ }$,若沿图中虚线DE截去$∠A$,则$∠1+∠2=$______.
(2)如图2,翻折后,点A落在点$A'$处,若$∠1+∠2=110^{\circ }$,求$∠B+∠C$的度数.
(3)如图3,将$△ABC$沿DE折叠,使点A落在点$A'$处,若$∠1=80^{\circ },∠2=28^{\circ }$,则$∠A$的度数为______.

答案:
(1)$\because ∠A=60^{\circ },\therefore ∠ADE+∠AED=180^{\circ }-60^{\circ }=120^{\circ },\therefore ∠1+∠2=360^{\circ }-∠ADE-∠AED=240^{\circ }$,故答案为:$240^{\circ }$.
(2)连结$AA'$,如图1所示,$\because ∠1=∠DAA'+∠DA'A,∠2=∠EAA'+∠EA'A,\therefore ∠1+∠2=∠DAA'+∠DA'A+∠EAA'+∠EA'A=∠EAD+∠EA'D$. $\because ∠EAD=∠EA'D,\therefore ∠1+∠2=2∠EAD=110^{\circ },\therefore ∠EAD=55^{\circ },\therefore ∠B+∠C=180^{\circ }-55^{\circ }=125^{\circ }$.
(3)如图2,设 AB 与$DA'$交于点 F,$\because ∠1=∠DFA+∠A,∠DFA=∠2+∠A'$,由折叠可得,$\angle A=\angle {A}^{\prime },\therefore \angle 1=\angle A+\angle {A}^{\prime }+\angle 2=2\angle A+∠2$. 又$\because ∠1=80^{\circ },∠2=28^{\circ },\therefore 80^{\circ }=2∠A+28^{\circ },\therefore ∠A=26^{\circ }$. 故答案为:$26^{\circ }$.
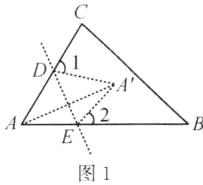

(1)$\because ∠A=60^{\circ },\therefore ∠ADE+∠AED=180^{\circ }-60^{\circ }=120^{\circ },\therefore ∠1+∠2=360^{\circ }-∠ADE-∠AED=240^{\circ }$,故答案为:$240^{\circ }$.
(2)连结$AA'$,如图1所示,$\because ∠1=∠DAA'+∠DA'A,∠2=∠EAA'+∠EA'A,\therefore ∠1+∠2=∠DAA'+∠DA'A+∠EAA'+∠EA'A=∠EAD+∠EA'D$. $\because ∠EAD=∠EA'D,\therefore ∠1+∠2=2∠EAD=110^{\circ },\therefore ∠EAD=55^{\circ },\therefore ∠B+∠C=180^{\circ }-55^{\circ }=125^{\circ }$.
(3)如图2,设 AB 与$DA'$交于点 F,$\because ∠1=∠DFA+∠A,∠DFA=∠2+∠A'$,由折叠可得,$\angle A=\angle {A}^{\prime },\therefore \angle 1=\angle A+\angle {A}^{\prime }+\angle 2=2\angle A+∠2$. 又$\because ∠1=80^{\circ },∠2=28^{\circ },\therefore 80^{\circ }=2∠A+28^{\circ },\therefore ∠A=26^{\circ }$. 故答案为:$26^{\circ }$.


查看更多完整答案,请扫码查看


