《2025年暑假衔接八年级数学浙教版延边人民出版社》

14. 如图,点$A$,$D$,$C$,$F$在同一条直线上,$AD = CF$,$AB = DE$,$BC = EF$.
(1)求证:$\triangle ABC\cong \triangle DEF$.
证明:∵AD = CF,∴AD + DC = CF + DC,即AC = DF.又∵AB = DE,BC = EF,∴△ABC ≌ △DEF(SSS).
(2)求证:$AB// DE$.
证明:∵△ABC ≌ △DEF,∴∠BAC = ∠EDF,∴AB // DE.

答案：
(1)证明:
∵AD = CF,
∴AD + DC = CF + DC,即AC = DF.又
∵AB = DE,BC = EF,
∴△ABC ≌ △DEF(SSS).
(2)证明:
∵△ABC ≌ △DEF,
∴∠BAC = ∠EDF,
∴AB // DE.

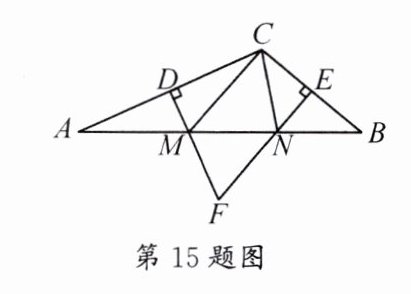
15. 如图,在$\triangle ABC$中,$DM$,$EN$分别垂直平分$AC$和$BC$,交$AB$于$M$,$N$两点,$DM$与$EN$相交于点$F$.
(1)若$\triangle CMN$的周长为$15cm$,求$AB$的长.15cm
(2)若$\angle MFN = 70^{\circ}$,求$\angle MCN$的度数.40°

答案：
(1)
∵DM,EN分别垂直平分AC和BC,
∴AM = CM,BN = CN,
∴△CMN的周长 = CM + MN + CN = AM + MN + BN = AB.
∵△CMN的周长为15cm,
∴AB = 15cm
(2)
∵∠MFN = 70°,
∴∠MNF + ∠NMF = 180° - 70° = 110°.
∵∠AMD = ∠NMF,∠BNE = ∠MNF,
∴∠AMD + ∠BNE = ∠MNF + ∠NMF = 110°,
∴∠A + ∠B = 90° - ∠AMD + 90° - ∠BNE = 180° - 110° = 70°.
∵AM = CM;BN = CN,
∴∠A = ∠ACM,∠B = ∠BCN,
∴∠MCN = 180° - 2(∠A + ∠B)=180° - 2×70° = 40°.

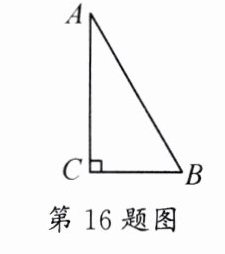
16. 如图,$\triangle ABC$中,$\angle C = 90^{\circ}$,$AB = 5cm$,$BC = 3cm$,若动点$P$从点$C$开始,按$C\rightarrow A\rightarrow B\rightarrow C$的路径运动,且速度为每秒$1cm$,设出发的时间为$t$秒.
(1)出发$2$秒后,求$\triangle ABP$的周长.
(2)问$t$为何值时,$\triangle BCP$为等腰三角形?
(3)另有一点$Q$,从点$C$开始,按$C\rightarrow A\rightarrow B\rightarrow C$的路径运动,且速度为每秒$2cm$,若$P$,$Q$两点同时出发,当$P$,$Q$中有一点到达终点时,另一点也停止运动. 当$t$为何值时,直线$PQ$把$\triangle ABC$的周长分成相等的两部分?

答案：

(1)如图1,由∠C = 90°,AB = 5cm,BC = 3cm,
∴AC = 4cm.动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,
∴出发2秒后,CP = 2cm,
∴AP = 2cm.
∵∠C = 90°,
∴PB = $\sqrt{2²+3²}$ = $\sqrt{13}$(cm),
∴△ABP的周长为AP + PB + AB = 2 + 5 + $\sqrt{13}$ = (7 + $\sqrt{13}$)cm.
(2)①如图2,若点P在边AC上时,BC = CP = 3cm,此时用的时间为3秒;②若点P在AB边上时,有三种情况:(i)如图3,若BP = CB = 3cm,此时AP = 2cm,点P运动的路程为2 + 4 = 6(cm),所以用的时间为6秒;(ii)如图4,若CP = BC = 3cm,作CD⊥AB于点D,
∵$\frac{1}{2}$AC·BC = $\frac{1}{2}$AB·CD,
∴CD = 2.4cm,在Rt△PCD中,PD = $\sqrt{PC² - CD²}$ = $\sqrt{3² - 2.4²}$ = 1.8(cm),所以BP = 2PD = 3.6cm,所以点P运动的路程为9 - 3.6 = 5.4(cm),则用的时间为5.4秒;(iii)如图5,若BP = CP,此时P应该为斜边AB的中点,点P运动的路程为4 + 2.5 = 6.5cm,则所用的时间为6.5秒;综上所述,当t为3或5.4或6或6.5时,△BCP为等腰三角形.
(3)
∵△ABC的周长为3 + 4 + 5 = 12(cm),
∴△ABC周长的一半为6cm,如图6,当点P在AC上(0＜t ≤ 4),点Q在AB上,则PC = t,BQ = 9 - 2t.
∵直线PQ把△ABC的周长分成相等的两部分,
∴t + 9 - 2t + 3 = 6,解得t = 6(舍去);如图7,当点P在AB上(4＜t ≤ 6),点Q在BC上,则AP = t - 4,CQ = 12 - 2t.
∵直线PQ把△ABC的周长分成相等的两部分,
∴t - 4 + 12 - 2t + 4 = 6,解得t = 6,
∴当t为6秒时,直线PQ把△ABC的周长分成相等的两部分.