2025年暑假衔接八年级数学浙教版延边人民出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假衔接八年级数学浙教版延边人民出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第14页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
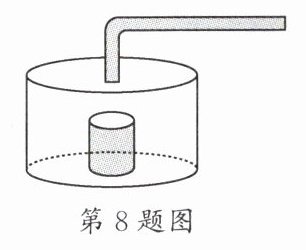
8. 小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器.然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出容器最高水位$h$与注水时间$t$之间的变化情况的是(
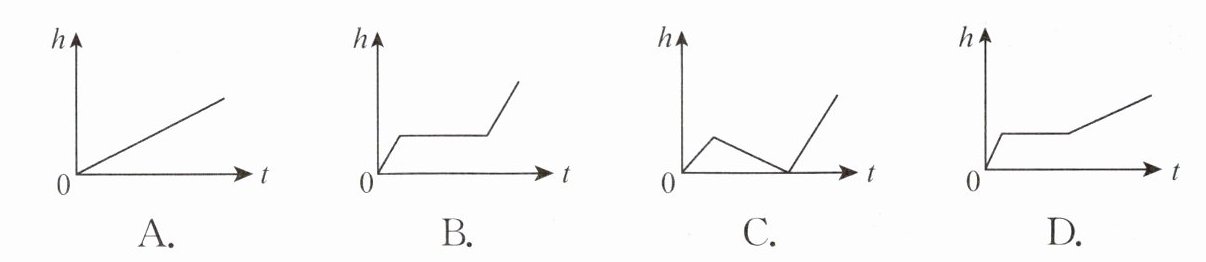
D
)

答案:
D [解析]注水管向小玻璃杯内注水,水面在逐渐升高,当注满玻璃杯后,水开始向鱼缸内流,此时最高水位不变,直到鱼缸水面高度与玻璃杯水面高度相同;当鱼缸水面高度与玻璃杯水面高度一样后,再继续注水,水位继续升高,但升高的速度变慢。故选:D。
9. 若点$(-2,y_1)$,$(2,y_2)$都在直线$y = -2x + 6$上,则$y_1$
>
$y_2$.(填“$<$”“$>$”或“$=$”)
答案:
>
10. 若点$A(m + 2,2m - 5)$在$y$轴上,则$m =$
−2
.
答案:
−2
11. 将一次函数$y = 3x + 2$的图象向下平移1个单位长度后得到的函数表达式为
y = 3x + 1
.
答案:
y = 3x + 1
12. 某饮料厂生产一种饮料,经测算,用1吨水生产的饮料所获利润$y$(元)与1吨水的买入价$x$(元)的关系如下表:
|1吨水的买入价$x$/元|2|4|6|8|10|
|----|----|----|----|----|----|
|利润$y$/元|202|200|198|196|194|
当用1吨水生产的饮料所获的利润$y$为190元时,买入1吨水需要
|1吨水的买入价$x$/元|2|4|6|8|10|
|----|----|----|----|----|----|
|利润$y$/元|202|200|198|196|194|
当用1吨水生产的饮料所获的利润$y$为190元时,买入1吨水需要
14
元.
答案:
14
13. 如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“$\to$”方向排列,如$(1,0)$,$(2,0)$,$(2,1)$,$(3,2)$,$(3,1)$,$(3,0)$,$\cdots$,已知$(1,0)$是第1个点,则第74个点的坐标为____
(12,7)
.
答案:
(12,7) [解析]观察图形可知,横坐标是1的点有1个,横坐标是2的点有2个,横坐标是3的点有3个……横坐标为奇数时,点的运动方向是从上往下,横坐标为偶数时,点的运动方向是从下往上;
∵74=(1 + 2 + 3 +... + 11)+8,
∴第74个点的横坐标为11 + 1 = 12,纵坐标为8 - 1 = 7,
∴第74个点的坐标为(12,7)。故答案为:(12,7)。
∵74=(1 + 2 + 3 +... + 11)+8,
∴第74个点的横坐标为11 + 1 = 12,纵坐标为8 - 1 = 7,
∴第74个点的坐标为(12,7)。故答案为:(12,7)。
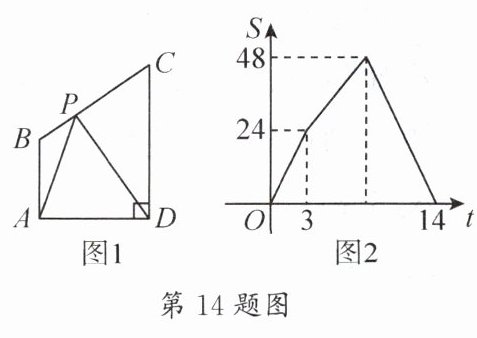
14. 如图1,四边形$ABCD$中,$AB// CD$,$\angle ADC = 90^{\circ}$,点$P$从点$A$出发,以每秒两个单位长度的速度,按$A - B - C - D$的顺序在边上匀速运动,设点$P$的运动时间为$t$秒,$\triangle PAD$的面积为$S$,$S$关于$t$的函数图象如图所示,当点$P$运动____
$\frac{11}{2}$或$\frac{19}{2}$
秒时,$\triangle APD$的面积为36.
答案:
$\frac{11}{2}$或$\frac{19}{2}$ [解析]根据函数图象可得AB = 3×2 = 6,AD = $\frac{2×24}{6}$ = 8,
∵当点P运动到点C时,AB + BC = 2t,
∴BC = 2t - AB = 2t - 6。
∵总时间为14秒,速度为每秒两个单位长度,
∴CD = 14×2 - 2t = 28 - 2t。
∵当点P运动到点C时,△APD的面积取得最大值,最大值为48。
∴$\frac{1}{2}$AD×DC = 48,
∴CD = 12,
∴28 - 2t = 12,解得t = 8,可解得图2中分段函数的表达式为$S = \begin{cases}8t(0\leqslant t\leqslant3),\\\frac{24}{5}t + \frac{48}{5}(3\lt t\leqslant8),\\-8t + 112(8\lt t\leqslant14),\end{cases}$当S = 36时,只有$\frac{24}{5}t + \frac{48}{5} = 36$或$-8t + 112 = 36$,解得$t = \frac{11}{2}$或$t = \frac{19}{2}$。故答案为:$\frac{11}{2}$或$\frac{19}{2}$。
∵当点P运动到点C时,AB + BC = 2t,
∴BC = 2t - AB = 2t - 6。
∵总时间为14秒,速度为每秒两个单位长度,
∴CD = 14×2 - 2t = 28 - 2t。
∵当点P运动到点C时,△APD的面积取得最大值,最大值为48。
∴$\frac{1}{2}$AD×DC = 48,
∴CD = 12,
∴28 - 2t = 12,解得t = 8,可解得图2中分段函数的表达式为$S = \begin{cases}8t(0\leqslant t\leqslant3),\\\frac{24}{5}t + \frac{48}{5}(3\lt t\leqslant8),\\-8t + 112(8\lt t\leqslant14),\end{cases}$当S = 36时,只有$\frac{24}{5}t + \frac{48}{5} = 36$或$-8t + 112 = 36$,解得$t = \frac{11}{2}$或$t = \frac{19}{2}$。故答案为:$\frac{11}{2}$或$\frac{19}{2}$。
查看更多完整答案,请扫码查看


