2025年暑假衔接八年级数学浙教版延边人民出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假衔接八年级数学浙教版延边人民出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第11页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
15. 解不等式(组):
(1)$\frac {x+3}{3}-\frac {2x-1}{2}>-3$。
(2)$\left\{\begin{array}{l} 2x-4≤3(x-1),\\ 2x+1>-5.\end{array}\right. $
(1)$\frac {x+3}{3}-\frac {2x-1}{2}>-3$。
(2)$\left\{\begin{array}{l} 2x-4≤3(x-1),\\ 2x+1>-5.\end{array}\right. $
答案:
(1)$\frac{x+3}{3}$−$\frac{2x−1}{2}$>−3,2(x+3)−3(2x−1)>−18,2x+6−6x+3>−18,−4x>−27,x<$\frac{27}{4}$.
(2)解不等式2x−4≤3(x−1)可得x≥−1,解不等式2x+1>−5可得x>−3,则不等式组的解集为x≥−1.
(1)$\frac{x+3}{3}$−$\frac{2x−1}{2}$>−3,2(x+3)−3(2x−1)>−18,2x+6−6x+3>−18,−4x>−27,x<$\frac{27}{4}$.
(2)解不等式2x−4≤3(x−1)可得x≥−1,解不等式2x+1>−5可得x>−3,则不等式组的解集为x≥−1.
16. 二月樱花开,四月樱桃红,随着樱桃成熟上市,某水果店花费6000元购进黄蜜樱桃,另花费1000元购进红灯樱桃,黄蜜樱桃的进价是红灯樱桃的进价的2倍,黄蜜樱桃的数量比红灯樱桃的数量多100千克。
(1)求红灯樱桃每千克的进价。
(2)该水果店第一周以40元/千克的价格售出红灯樱桃$3m$千克,第二周每千克售价降低了$0.5m$元,售出20千克,购进的红灯樱桃剩余部分全部以七折优惠售罄。若购进的红灯樱桃总利润不低于770元,求$m$的最小值。
(1)求红灯樱桃每千克的进价。
(2)该水果店第一周以40元/千克的价格售出红灯樱桃$3m$千克,第二周每千克售价降低了$0.5m$元,售出20千克,购进的红灯樱桃剩余部分全部以七折优惠售罄。若购进的红灯樱桃总利润不低于770元,求$m$的最小值。
答案:
(1)设红灯樱桃每千克的进价为x元,根据题意,得$\frac{6000}{2x}$−100=$\frac{1000}{x}$,解得x=20,经检验,x=20是原分式方程的根,答:红灯樱桃每千克的进价为20元.
(2)1000÷20=50(千克),根据题意,得(40−20)×3m+20(40−0.5m−20)+(40×0.7−20)×(50−3m−20)≥770,解得m≥5,答:m的最小值为5.
(1)设红灯樱桃每千克的进价为x元,根据题意,得$\frac{6000}{2x}$−100=$\frac{1000}{x}$,解得x=20,经检验,x=20是原分式方程的根,答:红灯樱桃每千克的进价为20元.
(2)1000÷20=50(千克),根据题意,得(40−20)×3m+20(40−0.5m−20)+(40×0.7−20)×(50−3m−20)≥770,解得m≥5,答:m的最小值为5.
17. 阅读理解:
例1. 解方程$|x|=2$,因为在数轴上到原点的距离为2的点对应的数为$\pm 2$,所以方程$|x|=2$的解为$x=\pm 2$。
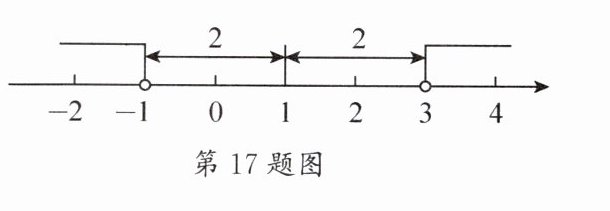
例2. 解不等式$|x-1|>2$,在数轴上找出$|x-1|=2$的解(如图),因为在数轴上到1对应的点的距离等于2的点对应的数为$-1$或3,所以方程$|x-1|=2$的解为$x=-1$或$x=3$,因此不等式$|x-1|>2$的解集为$x<-1$或$x>3$。
参考阅读材料,解答下列问题:
(1)方程$|x-2|=3$的解为__________。
(2)解不等式:$|x-2|≤1$。
(3)解不等式:$|x-4|+|x+2|>8$。
例1. 解方程$|x|=2$,因为在数轴上到原点的距离为2的点对应的数为$\pm 2$,所以方程$|x|=2$的解为$x=\pm 2$。
例2. 解不等式$|x-1|>2$,在数轴上找出$|x-1|=2$的解(如图),因为在数轴上到1对应的点的距离等于2的点对应的数为$-1$或3,所以方程$|x-1|=2$的解为$x=-1$或$x=3$,因此不等式$|x-1|>2$的解集为$x<-1$或$x>3$。
参考阅读材料,解答下列问题:

(1)方程$|x-2|=3$的解为__________。
(2)解不等式:$|x-2|≤1$。
(3)解不等式:$|x-4|+|x+2|>8$。
答案:
(1)
∵在数轴上到2对应的点的距离等于3的点对应的数为−1或5,
∴方程|x−2|=3的解为x=−1或x=5,故答案为:x=−1或x=5.

(2)在数轴上找出|x−2|=1的解,如图,
∵在数轴上到2对应的点的距离等于1的点对应的数为1或3,
∴方程|x−2|=1的解为x=1或x=3,
∴不等式|x−2|≤1的解集为1≤x≤3.
(3)在数轴上找出|x−4|+|x+2|=8的解,由绝对值的几何意义知,该方程就是求在数轴上到4和−2对应的点的距离之和等于8的点对应的x的值,
∵在数轴上4和−2对应的点的距离为6,
∴满足方程的x对应的点在4的右边或−2的左边,若x对应的点在4的右边,可得x=5;若x对应的点在−2的左边,可得x=−3,
∴方程|x−4|+|x+2|=8的解是x=5或x=−3,
∴不等式|x−4|+|x+2|>8的解集为x>5或x<−3.
(1)
∵在数轴上到2对应的点的距离等于3的点对应的数为−1或5,
∴方程|x−2|=3的解为x=−1或x=5,故答案为:x=−1或x=5.

(2)在数轴上找出|x−2|=1的解,如图,
∵在数轴上到2对应的点的距离等于1的点对应的数为1或3,
∴方程|x−2|=1的解为x=1或x=3,
∴不等式|x−2|≤1的解集为1≤x≤3.
(3)在数轴上找出|x−4|+|x+2|=8的解,由绝对值的几何意义知,该方程就是求在数轴上到4和−2对应的点的距离之和等于8的点对应的x的值,
∵在数轴上4和−2对应的点的距离为6,
∴满足方程的x对应的点在4的右边或−2的左边,若x对应的点在4的右边,可得x=5;若x对应的点在−2的左边,可得x=−3,
∴方程|x−4|+|x+2|=8的解是x=5或x=−3,
∴不等式|x−4|+|x+2|>8的解集为x>5或x<−3.
查看更多完整答案,请扫码查看


