《2025年暑假衔接八年级数学浙教版延边人民出版社》

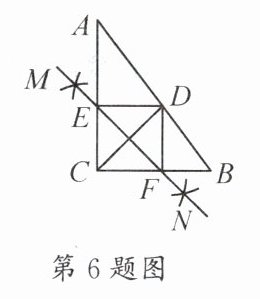
6. 如图,$ \mathrm { Rt } \triangle A B C $ 中,$ \angle A C B = 90 ^ { \circ } $,$ C D $ 平分 $ \angle A C B $ 交 $ A B $ 于点 $ D $,按下列步骤作图.
步骤 1:分别以点 $ C $ 和点 $ D $ 为圆心,以大于 $ \frac { 1 } { 2 } C D $ 的长为半径画弧,两弧相交于 $ M , N $ 两点;
步骤 2:作直线 $ M N $,分别交 $ A C , B C $ 于点 $ E , F $;
步骤 3:连结 $ D E , D F $.
若 $ A C = 8 $,$ B C = 6 $,则线段 $ D E $ 的长为 …………………………… (D)

A. $ \frac { 3 } { 2 } $ B. $ \frac { 12 } { 7 } $ C. $ \sqrt { 2 } $ D. $ \frac { 24 } { 7 } $

答案： D

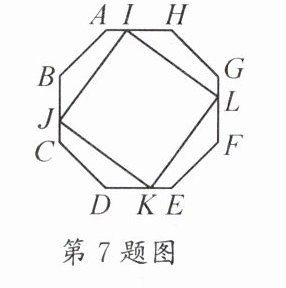
7. 如图,在边长为 $ \sqrt { 2 } $ 的正八边形 $ A B C D E F G H $ 中,已知 $ I , J , K , L $ 分别是边 $ A H , B C , D E , F G $ 上的动点,且满足 $ I A = J C = K E = L G $,则四边形 $ I J K L $ 面积的最大值为 ………………… ( )

A. $ 4 + 2 \sqrt { 2 } $ B. $ 2 + 2 \sqrt { 2 } $ C. $ 4 + \sqrt { 2 } $ D. $ 2 + 4 \sqrt { 2 } $

答案：
A　[解析]如图1,连结IK,JL,
∵正八边形，IA=JC=KE=LG,易得IJ=JK=KL=LI,IK=JL,
∴四边形IJKL为正方形，
∴四边形IJKL的面积为IJ².当IJ最大时,四边形IJKL 的面积最大，
∴当IJ=AC,即IJ为正八边形的对角线时，四边形IJKL的面积最大.如图2,连结AE,CG交于点O,连结OB,交AC于点M,则△AOC为等腰直角三角形，O为正八边形的中心，
∴OC=OB=OA,OB垂直平分AC,
∴OM=AM=$\frac{\sqrt{2}}{2}$OA.设OM=AM=x,则OC=OB=OA=$\sqrt{2}$x,
∴BM=$\sqrt{2}$x−x,在Rt△AMB中,AB²=BM²+AM²,即($\sqrt{2}$)²=($\sqrt{2}$x−x)² + x²,解得x=$\frac{\sqrt{2\sqrt{2}+4}}{2}$(负值不合题意，已舍去),
∴AC=2AM=$\sqrt{2\sqrt{2}+4}$,
∴四边形IJKL的最大面积为AC²=4+2$\sqrt{2}$;故选:A.
　　

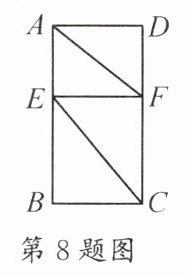
8. 如图,矩形 $ A B C D $ 中,$ A B = 8 $,$ A D = 4 $,$ E , F $ 分别是 $ A B , D C $ 上的动点,$ E F // B C $,则 $ A F + C E $ 的最小值是 …………………………… (A)

A. $ 8 \sqrt { 2 } $ B. 12 C. $ 8 \sqrt { 5 } $ D. 16

答案： A　[解析]如图,作点A关于CD的对称点G,连结BG,FG,BF,则AF=FG,AD=DG,在矩形ABCD中，AB//CD,∠B=∠BAD=90°.
∵EF//BC,
∴四边形BEFC是平行四边形.
∵∠ABC=90°,
∴四边形BEFC是矩形,
∴CE=BF,
∴AF+CE的最小值等于AF+BF的最小值，等于GF十BF的最小值，即BG的长度.
∵AB=8,AD=4,
∴AG=8.根据勾股定理，得BG=$\sqrt{AB²+AG²}$=8$\sqrt{2}$,
∴AF+CE的最小值为8$\sqrt{2}$,故选:A

9. 要用反证法证明:“如果一个三角形的两条较短边的平方和不等于较长边的平方,那么这个三角形不是直角三角形.”第一步应假设这个三角形是直角三角形.

答案： 这个三角形是直角三角形

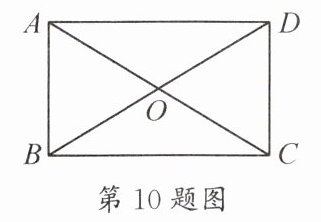
10. 如图,矩形 $ A B C D $ 的对角线 $ A C , B D $ 交于点 $ O $,若 $ \angle A O D = 100 ^ { \circ } $,则 $ \angle O A B = $50$ ^ { \circ } $.

答案： 50

11. 如图,在 $ \triangle A B C $ 中,$ D , E $ 分别是 $ A C , B C $ 的中点,以 $ A $ 为圆心,$ A D $ 长为半径作圆弧交 $ A B $ 于点 $ F $,若 $ A D = 8 $,$ D E = 7 $,则 $ B F $ 的长为______6______.

答案： 6

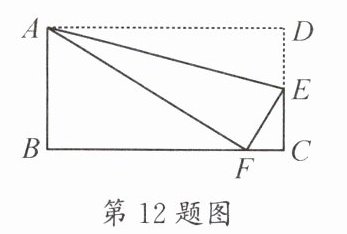
12. 如图,将一张矩形纸片沿着 $ A E $ 折叠后,点 $ D $ 恰好与 $ B C $ 边上的点 $ F $ 重合,已知 $ A B = 6 \mathrm { cm } $,$ B C = 10 \mathrm { cm } $,则 $ E C $ 的长度为$\frac{8}{3}$$ \mathrm { cm } $.

答案： $\frac{8}{3}$