2025年暑假衔接八年级数学浙教版延边人民出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假衔接八年级数学浙教版延边人民出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第15页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
15. 已知,点$P(2m - 6,m + 2)$.
(1)若点$P$在$x$轴上,求$m$的值及点$P$的坐标.
(2)若点$P$的横、纵坐标互为相反数,求点$P$在第几象限.
(3)若点$P$和点$Q$都在过点$A(2,3)$且与$y$轴平行的直线上,$PQ = 4$,求点$Q$的坐标.
(1)若点$P$在$x$轴上,求$m$的值及点$P$的坐标.
(2)若点$P$的横、纵坐标互为相反数,求点$P$在第几象限.
(3)若点$P$和点$Q$都在过点$A(2,3)$且与$y$轴平行的直线上,$PQ = 4$,求点$Q$的坐标.
答案:
(1)
∵点P在x轴上,
∴m + 2 = 0,解得m = - 2,
∴2m - 6 = 2×(-2) - 6 = - 10,
∴点P的坐标为(-10,0)。
(2)根据题意得2m - 6 + m + 2 = 0,解得$m = \frac{4}{3}$,
∴$2m - 6 = 2\times\frac{4}{3} - 6 = -\frac{10}{3}\lt0$,$m + 2 = \frac{4}{3} + 2 = \frac{10}{3}\gt0$,
∴点P在第二象限。
(3)
∵点P和点Q都在过点A(2,3)且与y轴平行的直线上,
∴点P和点Q的横坐标都为2,
∴2m - 6 = 2,解得m = 4,
∴m + 2 = 6,
∴点P(2,6),
∵PQ = 4,
∴点Q的纵坐标为10或2,
∴点Q的坐标为(2,10)或(2,2)。
(1)
∵点P在x轴上,
∴m + 2 = 0,解得m = - 2,
∴2m - 6 = 2×(-2) - 6 = - 10,
∴点P的坐标为(-10,0)。
(2)根据题意得2m - 6 + m + 2 = 0,解得$m = \frac{4}{3}$,
∴$2m - 6 = 2\times\frac{4}{3} - 6 = -\frac{10}{3}\lt0$,$m + 2 = \frac{4}{3} + 2 = \frac{10}{3}\gt0$,
∴点P在第二象限。
(3)
∵点P和点Q都在过点A(2,3)且与y轴平行的直线上,
∴点P和点Q的横坐标都为2,
∴2m - 6 = 2,解得m = 4,
∴m + 2 = 6,
∴点P(2,6),
∵PQ = 4,
∴点Q的纵坐标为10或2,
∴点Q的坐标为(2,10)或(2,2)。
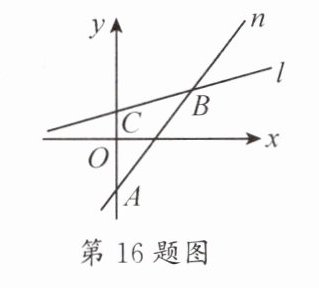
16. 在如图所示的平面直角坐标系中,直线$n$过点$A(0,-2)$且与直线$l$交于点$B(3,2)$,直线$l$与$y$轴正半轴交于点$C$.
(1)求直线$n$的函数表达式.
(2)若$\triangle ABC$的面积为9,求点$C$的坐标.
(3)若$\triangle ABC$是以$AB$为底的等腰三角形,求直线$l$的函数表达式.
(1)求直线$n$的函数表达式.
(2)若$\triangle ABC$的面积为9,求点$C$的坐标.
(3)若$\triangle ABC$是以$AB$为底的等腰三角形,求直线$l$的函数表达式.

答案:
(1)设直线n的表达式为y = kx + b,
∵直线n:y = kx + b过点A(0,-2),B(3,2),
∴$\begin{cases}b = - 2,\\2 = 3k - 2,\end{cases}$解得$\begin{cases}b = - 2,\\k = \frac{4}{3},\end{cases}$
∴直线n的函数表达式为$y = \frac{4}{3}x - 2$。
(2)
∵△ABC的面积为9,点B(3,2),
∴9 = $\frac{1}{2}$×AC×3,
∴AC = 6,
∵点A(0,-2),
∴OA = 2,
∴OC = 6 - 2 = 4,
∴点C(0,4)。
(3)
∵△ABC是以AB为底的等腰三角形,
∴AC = BC,过点B作BD⊥y轴于点D,如图。
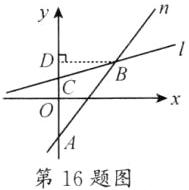
∵点A(0,-2),B(3,2),
∴AD = 4,BD = 3,设AC = a,则BC = a,CD = 4 - a,在Rt△BCD中,由勾股定理得$BD^{2} + CD^{2} = BC^{2}$,
∴$3^{2} + (4 - a)^{2} = a^{2}$,解得$a = \frac{25}{8}$,
∴OC = $\frac{25}{8} - 2 = \frac{9}{8}$,
∴点$C(0,\frac{9}{8})$,设直线l的表达式为y = mx + n,把点$C(0,\frac{9}{8})$,B(3,2)代入得$\begin{cases}n = \frac{9}{8},\\2 = 3m + n,\end{cases}$解得$\begin{cases}m = \frac{7}{24},\\n = \frac{9}{8},\end{cases}$直线l的表达式为$y = \frac{7}{24}x + \frac{9}{8}$。
(1)设直线n的表达式为y = kx + b,
∵直线n:y = kx + b过点A(0,-2),B(3,2),
∴$\begin{cases}b = - 2,\\2 = 3k - 2,\end{cases}$解得$\begin{cases}b = - 2,\\k = \frac{4}{3},\end{cases}$
∴直线n的函数表达式为$y = \frac{4}{3}x - 2$。
(2)
∵△ABC的面积为9,点B(3,2),
∴9 = $\frac{1}{2}$×AC×3,
∴AC = 6,
∵点A(0,-2),
∴OA = 2,
∴OC = 6 - 2 = 4,
∴点C(0,4)。
(3)
∵△ABC是以AB为底的等腰三角形,
∴AC = BC,过点B作BD⊥y轴于点D,如图。

∵点A(0,-2),B(3,2),
∴AD = 4,BD = 3,设AC = a,则BC = a,CD = 4 - a,在Rt△BCD中,由勾股定理得$BD^{2} + CD^{2} = BC^{2}$,
∴$3^{2} + (4 - a)^{2} = a^{2}$,解得$a = \frac{25}{8}$,
∴OC = $\frac{25}{8} - 2 = \frac{9}{8}$,
∴点$C(0,\frac{9}{8})$,设直线l的表达式为y = mx + n,把点$C(0,\frac{9}{8})$,B(3,2)代入得$\begin{cases}n = \frac{9}{8},\\2 = 3m + n,\end{cases}$解得$\begin{cases}m = \frac{7}{24},\\n = \frac{9}{8},\end{cases}$直线l的表达式为$y = \frac{7}{24}x + \frac{9}{8}$。
17. 一艘轮船在航行中遇到暗礁,船身有一处出现进水现象,等到发现时,船内已有一定积水,船员立即开始自救,一边排水一边修船,在整个过程中进水速度不变,同时修船过程中排水速度不变,船修好后不再进水,此时的排水速度与修船过程中进水速度相同,直到将船内积水排尽,设轮船触礁后船舱内积水量为$y(\text{t})$,时间为$x(\text{min})$,$y$与$x$之间的函数图象如图所示.
(1)修船过程中排水速度为
(2)求修船完工后$y$与$x$之间的函数关系式,并写出自变量$x$的取值范围.
(3)当船内积水量是船内最高积水量的$\frac{3}{4}$时,直接写出$x$的值.
(1)修船过程中排水速度为
1
$\text{t}/\text{min}$,$a$的值为24
.(2)求修船完工后$y$与$x$之间的函数关系式,并写出自变量$x$的取值范围.
(3)当船内积水量是船内最高积水量的$\frac{3}{4}$时,直接写出$x$的值.
答案:
(1)进水速度为$\frac{20}{5} = 4(t/min)$,排水速度为$\frac{(13 - 5)\times4 - (44 - 20)}{13 - 5} = 1(t/min)$,
∵船修好后不再进水,此时的排水速度与修船过程中进水速度相同,
∴a = 13 + 44÷4 = 24。故答案为:1;24。
(2)设修船完工后y与x之间的函数关系式为y = kx + b(k≠0),根据题意得$\begin{cases}24k + b = 0,\\13k + b = 44,\end{cases}$解得$\begin{cases}k = - 4,\\b = 96,\end{cases}$
∴修船完工后y与x之间的函数关系式为y = - 4x + 96(13≤x≤24)。
(3)设修船过程中y与x之间的函数关系式为$y = k'x + b'(k'\neq0)$,根据题意得$\begin{cases}5k' + b' = 20,\\13k' + b' = 44,\end{cases}$解得$\begin{cases}k' = 3,\\b' = 5,\end{cases}$
∴修船过程中y与x之间的函数关系式为y = 3x + 5(5≤x≤13),当修船过程中,船内积水量是船内最高积水量的$\frac{3}{4}$时,根据题意得$3x + 5 = 44\times\frac{3}{4}$,解得$x = \frac{28}{3}$;当船修好后不再进水,船内积水量是船内最高积水量的$\frac{3}{4}$时,根据题意得$- 4x + 96 = 44\times\frac{3}{4}$,解得$x = \frac{63}{4}$;综上分析可知,当$x = \frac{28}{3}$或$x = \frac{63}{4}$时,船内积水量是船内最高积水量的$\frac{3}{4}$。
(1)进水速度为$\frac{20}{5} = 4(t/min)$,排水速度为$\frac{(13 - 5)\times4 - (44 - 20)}{13 - 5} = 1(t/min)$,
∵船修好后不再进水,此时的排水速度与修船过程中进水速度相同,
∴a = 13 + 44÷4 = 24。故答案为:1;24。
(2)设修船完工后y与x之间的函数关系式为y = kx + b(k≠0),根据题意得$\begin{cases}24k + b = 0,\\13k + b = 44,\end{cases}$解得$\begin{cases}k = - 4,\\b = 96,\end{cases}$
∴修船完工后y与x之间的函数关系式为y = - 4x + 96(13≤x≤24)。
(3)设修船过程中y与x之间的函数关系式为$y = k'x + b'(k'\neq0)$,根据题意得$\begin{cases}5k' + b' = 20,\\13k' + b' = 44,\end{cases}$解得$\begin{cases}k' = 3,\\b' = 5,\end{cases}$
∴修船过程中y与x之间的函数关系式为y = 3x + 5(5≤x≤13),当修船过程中,船内积水量是船内最高积水量的$\frac{3}{4}$时,根据题意得$3x + 5 = 44\times\frac{3}{4}$,解得$x = \frac{28}{3}$;当船修好后不再进水,船内积水量是船内最高积水量的$\frac{3}{4}$时,根据题意得$- 4x + 96 = 44\times\frac{3}{4}$,解得$x = \frac{63}{4}$;综上分析可知,当$x = \frac{28}{3}$或$x = \frac{63}{4}$时,船内积水量是船内最高积水量的$\frac{3}{4}$。
查看更多完整答案,请扫码查看


