《2025年暑假作业四年级南方日报出版社》

2. 小明家有一块三角形的菜地(如右下图)。为了防止小鸭子来偷吃瓜,小明的妈妈决定在菜地周围围上篱笆,请你帮他算一算需要多少钱。

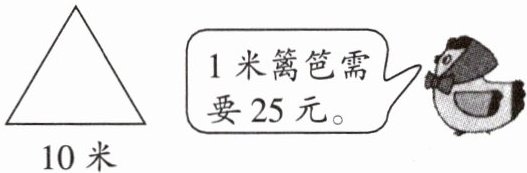
答案： 解：由图可知三角形菜地为等边三角形，边长为10米。
周长：10×3=30（米）
费用：30×25=750（元）
答：需要750元。

3. 三角形ABC的周长是78厘米,$∠B= ∠C,BC= 14$厘米,求AB的长。

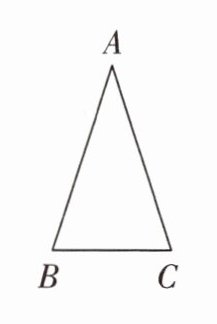
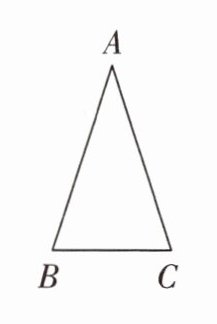
答案： 【解析】：题目考查等腰三角形的性质和周长计算。已知∠B=∠C，根据“等角对等边”可知AB=AC。三角形ABC的周长是78厘米，BC=14厘米，周长等于AB+BC+AC，因为AB=AC，所以周长可表示为2×AB+BC，由此可计算AB的长度。
【答案】：因为∠B=∠C，所以AB=AC。
三角形ABC的周长=AB+BC+AC=2×AB+BC。
已知周长为78厘米，BC=14厘米，
则2×AB+14=78，
2×AB=78-14=64，
AB=64÷2=32（厘米）。
答：AB的长是32厘米。

4. 右下图的三角形中,$∠1= 35^{\circ },∠2+∠3= 90^{\circ }$,求$∠2$、$∠3和∠4$的度数。

答案： 【解析】：本题考查三角形内角和定理（三角形内角和为180°）。由图可知，∠1、∠2与直角（90°）构成一个三角形，所以∠1+∠2+90°=180°，已知∠1=35°，可求出∠2=180°-90°-35°=55°；又因为∠2+∠3=90°，所以∠3=90°-∠2=90°-55°=35°；∠3、∠4与直角（90°）构成另一个三角形，故∠3+∠4+90°=180°，则∠4=180°-90°-∠3=180°-90°-35°=55°。
【答案】：∠2=55°，∠3=35°，∠4=55°

七、数学小博士。
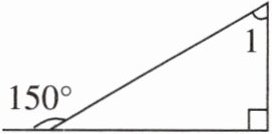
如右图,求$∠1$是多少度。

答案： 【解析】：题目考查三角形内角和为180°以及平角的概念。图中已知一个外角为150°，这个外角与三角形的一个内角组成平角（180°），所以先求出该内角为180° - 150° = 30°。又因为三角形有一个直角（90°），根据三角形内角和，∠1 = 180° - 90° - 30° = 60°。
【答案】：60°