《2025年暑假作业四年级南方日报出版社》

2. 小芳看一本180页的故事书,前3天平均每天看20页,剩下的部分如果要5天看完,平均每天要看多少页?

答案： 【解析】：本题考查整数的混合运算在实际问题中的应用。先计算前3天看的总页数，用每天看的页数乘天数，即$20×3$；再用总页数减去前3天看的页数得到剩下的页数，即$180 - 20×3$；最后用剩下的页数除以剩下的天数5天，得到平均每天要看的页数。
【答案】：
前3天看的页数：$20×3 = 60$（页）
剩下的页数：$180 - 60 = 120$（页）
平均每天看的页数：$120÷5 = 24$（页）
答：平均每天要看24页。

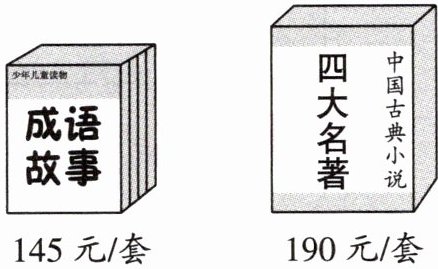
3. 某小学从书店购进《成语故事》和《四大名著》各两套,付了700元,还应找回多少元?

答案： 【解析】：本题考查整数的复合应用题，涉及单价、数量和总价的关系。首先需要明确《成语故事》和《四大名著》各自的单价，题目中通过插图给出《成语故事》145元/套，《四大名著》190元/套，各购进两套。先分别计算两种书的总价，再求和得到总花费，最后用付出的700元减去总花费，即可求出应找回的钱数。
计算过程：《成语故事》总价为 $145×2 = 290$ 元，《四大名著》总价为 $190×2 = 380$ 元，两种书总花费为 $290 + 380 = 670$ 元，应找回 $700 - 670 = 30$ 元。
【答案】：30元

4. 某校“六一”儿童节准备组织16位老师和134名学生去游玩,怎样租车最省钱?

答案： 【解析】：本题考查最优方案选择，涉及总人数计算、不同车型人均费用比较及租车方案设计。首先计算总人数：16位老师+134名学生=150人。接着比较大车和小车人均费用，大车人均900÷45=20元，小车人均660÷30=22元，故优先租大车更省钱。然后设计方案：150÷45=3辆……15人，余下15人租小车有空位，调整为租2辆大车（可坐90人），剩余60人租2辆小车（30×2=60人），刚好坐满。计算费用：2×900+2×660=1800+1320=3120元。
【答案】：租2辆大车和2辆小车最省钱，费用为3120元。

七、加上括号,使下列等式成立。
1. $7×9+12÷3= 91$
2. $48×6÷48×6= 1$
3. $7×9+12÷3= 49$

答案： 【解析】：本题考查整数的四则混合运算，需要通过添加括号改变运算顺序使等式成立。四则混合运算顺序为：先算乘除，后算加减，有括号的先算括号里的。
1. 对于$7×9 + 12÷3 = 91$，因为结果较大，考虑让$9 + 12÷3$先算，$9 + 12÷3 = 9 + 4 = 13$，$7×13 = 91$，所以添加括号为$7×(9 + 12÷3)$。
2. 对于$48×6÷48×6 = 1$，要使结果为1，考虑让$48×6$分别作为被除数和除数，即$(48×6)÷(48×6) = 288÷288 = 1$。
3. 对于$7×9 + 12÷3 = 49$，结果49是7×7，所以考虑让$9 + 12÷3$的结果为7，$9 + 12 = 21$，$21÷3 = 7$，所以添加括号为$7×[(9 + 12)÷3]$。
【答案】：1. $7×(9 + 12÷3)=91$
2. $(48×6)÷(48×6)=1$
3. $7×[(9 + 12)÷3]=49$