《2025年暑假零距离七年级数学人教版》

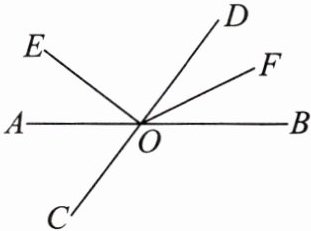
20. (9分)如图,直线$AB,CD交于点O$,$OF平分∠BOD$,$OE⊥OD$.
(1)若$∠BOF= 25^{\circ }$,求$∠AOE$的度数;
(2)若$∠AOE:∠AOC= 2:3$,求$∠BOF$的度数.

答案： 解:
(1)由条件可知 $\angle DOF = \angle BOF = 25^{\circ}$，
$\therefore \angle BOD = \angle DOF + \angle BOF = 50^{\circ}$。$\because OE \perp OD$，
$\therefore \angle EOD = 90^{\circ}$，$\therefore \angle AOE = 180^{\circ} - \angle DOE - \angle BOD = 180^{\circ} - 90^{\circ} - 50^{\circ} = 40^{\circ}$。
(2)由条件可知 $\angle EOC = 180^{\circ} - \angle EOD = 180^{\circ} - 90^{\circ} = 90^{\circ}$。$\because \angle AOE : \angle AOC = 2 : 3$，$\therefore \angle AOC = \frac{3}{5} × 90^{\circ} = 54^{\circ}$。$\because \angle AOC = \angle BOD$，$\therefore \angle BOD = 54^{\circ}$。$\because OF$ 平分 $\angle BOD$，$\therefore \angle BOF = \frac{1}{2}\angle BOD = \frac{1}{2} × 54^{\circ} = 27^{\circ}$。

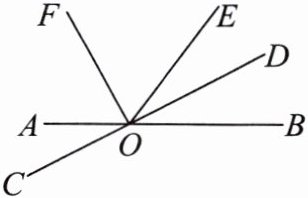
21. (9分)如图,直线$AB与CD相交于点O$,$OF$,$OD分别是∠AOE$,$∠BOE$的平分线.
(1)写出$∠DOE$的补角;
(2)试判断$OF和OD$的位置关系,并说明理由;
(3)若$∠BOE= 54^{\circ }$,求$∠AOD和∠EOF$的度数.

答案： 解:
(1) $\because OD$ 平分 $\angle BOE$，$\therefore \angle BOD = \angle DOE$，
$\therefore \angle DOE$ 的补角是 $\angle AOD$，$\angle BOC$，$\angle COE$。
(2) $OF \perp OD$。理由如下: $\because OF$，$OD$ 分别是 $\angle AOE$，$\angle BOE$ 的平分线，$\therefore \angle EOF = \frac{1}{2}\angle AOE$，
$\angle EOD = \frac{1}{2}\angle BOE$，$\therefore \angle EOF + \angle EOD = \frac{1}{2}(\angle AOE + \angle BOE)$，$\therefore \angle DOF = \frac{1}{2} × 180^{\circ} = 90^{\circ}$，$\therefore OD \perp OF$。
(3) $\because OD$ 平分 $\angle BOE$，$\therefore \angle BOD = \angle DOE = \frac{1}{2}\angle BOE = \frac{1}{2} × 54^{\circ} = 27^{\circ}$，$\therefore \angle AOD = 180^{\circ} - \angle BOD = 180^{\circ} - 27^{\circ} = 153^{\circ}$，$\angle EOF = 90^{\circ} - \angle EOD = 90^{\circ} - 27^{\circ} = 63^{\circ}$。

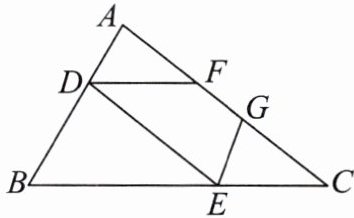
22. (10分)如图,三角形$ABC$中,$D是AB$上一点,$E是BC$上一点,点$F$,$G在AC$上,$∠AFD= ∠DEB$,$∠DFC+∠C= 180^{\circ }$.
(1)求证:$DE// AC$;
(2)若$∠C= 38^{\circ }$,$EG平分∠DEC$,求$∠EGC$的度数.

答案：
(1) 证明: $\because \angle DFC + \angle C = 180^{\circ}$，$\therefore DF // BC$，
$\therefore \angle DEB = \angle EDF$。$\because \angle AFD = \angle DEB$，$\therefore \angle EDF = \angle AFD$，$\therefore DE // AC$。
(2) 解: $\because DE // AC$，$\therefore \angle C + \angle DEC = 180^{\circ}$。$\because \angle C = 38^{\circ}$，$\therefore \angle DEC = 180^{\circ} - 38^{\circ} = 142^{\circ}$。$\because EG$ 平分 $\angle DEC$，$\therefore \angle DEG = \frac{1}{2}\angle DEC = 71^{\circ}$。$\because DE // AC$，
$\therefore \angle EGC = \angle DEG = 71^{\circ}$。

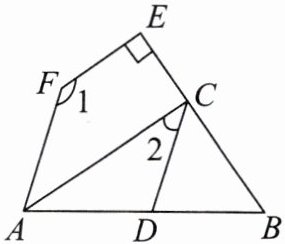
23. (12分)如图,已知$AC// FE$,$∠1+∠2= 180^{\circ }$.
(1)判断$∠FAB与∠BDC$的大小关系,并说明理由;
(2)若$AC平分∠FAD$,$EF⊥BE于点E$,$∠FAD= 74^{\circ }$,求$∠BCD$的度数.

答案： 解:
(1) $\angle FAB = \angle BDC$。理由如下: $\because AC // EF$，$\therefore \angle 1 + \angle FAC = 180^{\circ}$。$\because \angle 1 + \angle 2 = 180^{\circ}$，
$\therefore \angle FAC = \angle 2$，$\therefore FA // CD$，$\therefore \angle FAB = \angle BDC$。
(2) $\because AC$ 平分 $\angle FAD$，$\therefore \angle FAC = \frac{1}{2}\angle FAD = \frac{1}{2} × 74^{\circ} = 37^{\circ}$。由
(1)知 $\angle FAC = \angle 2$，$\therefore \angle 2 = 37^{\circ}$。
$\because EF \perp BE$，$AC // EF$，$\therefore AC \perp BE$，$\therefore \angle ACB = 90^{\circ}$，
$\therefore \angle BCD = \angle ACB - \angle 2 = 90^{\circ} - 37^{\circ} = 53^{\circ}$。