2025年暑假零距离七年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假零距离七年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
8. 如图,在△ABC中,过点B作PB⊥BC交边AC于点P,过点C作CQ⊥AB交AB的延长线于点Q,则图中线段

CQ
是△ABC的一条高.
答案:
$ CQ $
9. 如图,已知在直角△ABC中,BC边上有E,D,F三点,BD= CD,∠BAE= ∠DAE,AF⊥BC,垂足为F,则以AD为中线的三角形是

△ABC
;以AE为角平分线的三角形是△ABD
;以AF为高线的三角形有10
个.
答案:
$ \triangle ABC $ $ \triangle ABD $ 10
10. 如图,在△ABC中,点E是BC的中点,AB= 7,AC= 10,△ACE的周长是25,则△ABE的周长是______
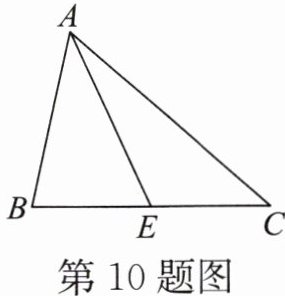
22
.
答案:
22
11. 已知△ABC的三边长是a,b,c.
(1) 若a= 4,b= 6,且三角形的周长是小于18的偶数,求c边的长;
(2) 化简|a+b-c|+|c-a-b|.
(1) 若a= 4,b= 6,且三角形的周长是小于18的偶数,求c边的长;
(2) 化简|a+b-c|+|c-a-b|.
答案:
解:
(1) $ \because a $,$ b $,$ c $ 是 $ \triangle ABC $ 的三边,$ a = 4 $,$ b = 6 $,$ \therefore 2 < c < 10 $。$ \because $ 三角形的周长是小于 18 的偶数,$ \therefore 2 < c < 8 $,$ \therefore c = 4 $ 或 6。
(2) 由三角形三边关系得 $ a + b - c > 0 $,$ c - a - b = c - (a + b) < 0 $,$ \therefore |a + b - c| + |c - a - b| = a + b - c - c + a + b = 2a + 2b - 2c $。
(1) $ \because a $,$ b $,$ c $ 是 $ \triangle ABC $ 的三边,$ a = 4 $,$ b = 6 $,$ \therefore 2 < c < 10 $。$ \because $ 三角形的周长是小于 18 的偶数,$ \therefore 2 < c < 8 $,$ \therefore c = 4 $ 或 6。
(2) 由三角形三边关系得 $ a + b - c > 0 $,$ c - a - b = c - (a + b) < 0 $,$ \therefore |a + b - c| + |c - a - b| = a + b - c - c + a + b = 2a + 2b - 2c $。
12. 如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,BF是∠ABC的平分线,BF与AE交于点O,若∠ABC= 40°,∠C= 60°,求∠DAE和∠BOE的度数.
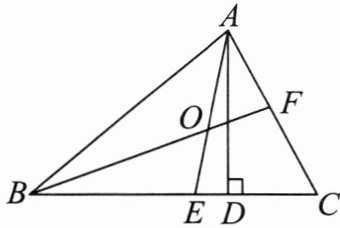

答案:
解:在$\triangle ABC$中,$\because \angle ABC=40^{\circ}$,$\angle C=60^{\circ}$,
$\therefore \angle BAC=180^{\circ}-\angle ABC-\angle C=180^{\circ}-40^{\circ}-60^{\circ}=80^{\circ}$。
$\because AE$是$\triangle ABC$的角平分线,
$\therefore \angle EAC=\frac{1}{2}\angle BAC=\frac{1}{2}×80^{\circ}=40^{\circ}$。
$\because AD$是$\triangle ABC$的高,
$\therefore \angle ADC=90^{\circ}$,
在$\triangle ADC$中,$\angle DAC=180^{\circ}-\angle ADC-\angle C=180^{\circ}-90^{\circ}-60^{\circ}=30^{\circ}$,
$\therefore \angle DAE=\angle EAC-\angle DAC=40^{\circ}-30^{\circ}=10^{\circ}$。
$\because BF$是$\angle ABC$的平分线,
$\therefore \angle FBC=\frac{1}{2}\angle ABC=\frac{1}{2}×40^{\circ}=20^{\circ}$,
在$\triangle BFC$中,$\angle BFC=180^{\circ}-\angle FBC-\angle C=180^{\circ}-20^{\circ}-60^{\circ}=100^{\circ}$,
$\therefore \angle AFO=180^{\circ}-\angle BFC=180^{\circ}-100^{\circ}=80^{\circ}$。
在$\triangle AOF$中,$\angle AOF=180^{\circ}-\angle AFO-\angle EAC=180^{\circ}-80^{\circ}-40^{\circ}=60^{\circ}$,
$\because \angle BOE$与$\angle AOF$是对顶角,
$\therefore \angle BOE=\angle AOF=60^{\circ}$。
综上,$\angle DAE=10^{\circ}$,$\angle BOE=60^{\circ}$。
$\therefore \angle BAC=180^{\circ}-\angle ABC-\angle C=180^{\circ}-40^{\circ}-60^{\circ}=80^{\circ}$。
$\because AE$是$\triangle ABC$的角平分线,
$\therefore \angle EAC=\frac{1}{2}\angle BAC=\frac{1}{2}×80^{\circ}=40^{\circ}$。
$\because AD$是$\triangle ABC$的高,
$\therefore \angle ADC=90^{\circ}$,
在$\triangle ADC$中,$\angle DAC=180^{\circ}-\angle ADC-\angle C=180^{\circ}-90^{\circ}-60^{\circ}=30^{\circ}$,
$\therefore \angle DAE=\angle EAC-\angle DAC=40^{\circ}-30^{\circ}=10^{\circ}$。
$\because BF$是$\angle ABC$的平分线,
$\therefore \angle FBC=\frac{1}{2}\angle ABC=\frac{1}{2}×40^{\circ}=20^{\circ}$,
在$\triangle BFC$中,$\angle BFC=180^{\circ}-\angle FBC-\angle C=180^{\circ}-20^{\circ}-60^{\circ}=100^{\circ}$,
$\therefore \angle AFO=180^{\circ}-\angle BFC=180^{\circ}-100^{\circ}=80^{\circ}$。
在$\triangle AOF$中,$\angle AOF=180^{\circ}-\angle AFO-\angle EAC=180^{\circ}-80^{\circ}-40^{\circ}=60^{\circ}$,
$\because \angle BOE$与$\angle AOF$是对顶角,
$\therefore \angle BOE=\angle AOF=60^{\circ}$。
综上,$\angle DAE=10^{\circ}$,$\angle BOE=60^{\circ}$。
13. 如图,在△ABC中(AB>BC),AC= 2BC,BC边上的中线AD把△ABC的周长分成70和50两部分,求AC和AB的长.
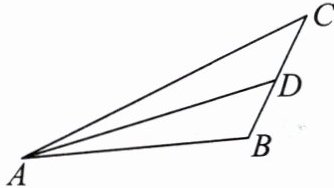

答案:
解:设 $ BD = CD = x $,则 $ AC = 2BC = 4x $。$ \because BC $ 边上的中线 $ AD $ 把 $ \triangle ABC $ 的周长分成 70 和 50 两部分,$ AB > BC $,$ \therefore $ ① 当 $ AC + CD = 70 $,$ AB + BD = 50 $ 时,$ 4x + x = 70 $,解得 $ x = 14 $,$ \therefore AC = 4x = 4 × 14 = 56 $,$ BD = CD = 14 $,$ \therefore AB = 50 - BD = 50 - 14 = 36 $,$ \therefore AB = 36 > BC = 28 $,满足条件。$ \because BC + AB = 36 + 28 = 64 > AC = 56 $,满足三边关系,$ \therefore AC = 56 $,$ AB = 36 $;
② 当 $ AC + CD = 50 $,$ AB + BD = 70 $ 时,$ 4x + x = 50 $,解得 $ x = 10 $,$ \therefore AC = 4x = 4 × 10 = 40 $,$ \therefore BD = CD = 10 $,$ AB = 70 - BD = 70 - 10 = 60 $。$ \because AC + BC = 60 = AB $,$ \therefore $ 不满足三角形的三边关系,舍去。
综上,$ AC = 56 $,$ AB = 36 $。
② 当 $ AC + CD = 50 $,$ AB + BD = 70 $ 时,$ 4x + x = 50 $,解得 $ x = 10 $,$ \therefore AC = 4x = 4 × 10 = 40 $,$ \therefore BD = CD = 10 $,$ AB = 70 - BD = 70 - 10 = 60 $。$ \because AC + BC = 60 = AB $,$ \therefore $ 不满足三角形的三边关系,舍去。
综上,$ AC = 56 $,$ AB = 36 $。
查看更多完整答案,请扫码查看


