《2025年暑假零距离七年级数学人教版》

7. 如图,在$\triangle ABC与\triangle ADE$中,$E在BC$边上,$AD = AB$,$AE = AC$,$DE = BC$,若$\angle 1 = 25^{\circ}$,则$\angle 2$的度数为$25^{\circ}$.

答案： $25^{\circ}$

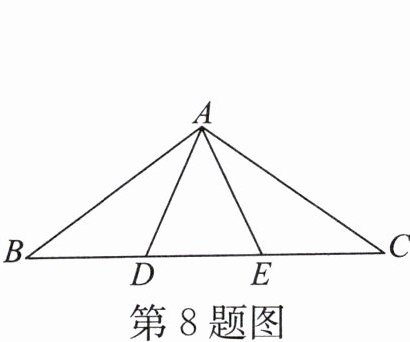
8. 如图,在$\triangle ABC$中,$AB = AC$,$D,E两点在BC$上,且$AD = AE$,$BD = CE$.若$\angle BAD = 30^{\circ}$,$\angle DAE = 50^{\circ}$,则$\angle BAC$的度数为$110^{\circ}$.
(插图编号：1.3-10) (插图编号：1.3-11)

答案： $110^{\circ}$

9. 如图,$AC = AD$,请你添加一个适当的条件:$BC = BD$（答案不唯一）,使得$\triangle ABC\cong \triangle ABD$.

答案： $BC = BD$（答案不唯一）

10. 在如图所示的6×5方格中,每个小方格都是边长为1的正方形,$\triangle ABC$是格点三角形(即顶点恰好是正方形的顶点),则与$\triangle ABC有一条公共边BC$且全等的所有格点三角形的个数是3个.

答案： 3

11. 如图,点$D,C在线段AF$上,$AD = CF$,$AB = DE$,$BC = EF$.
求证:$\triangle ABC\cong \triangle DEF$.
(插图编号：1.3-12)

答案： 证明：$\because AD = CF,\therefore AD + DC = CF + DC$，
$\therefore AC = DF$. 在$\triangle ABC$和$\triangle DEF$中，$\begin{cases}AB = DE,\\BC = EF,\\AC = DF,\end{cases}$
$\therefore \triangle ABC\cong\triangle DEF(SSS)$.

12. (1)思考:一个平分角的仪器如图1所示,其中$AB = AD$,$BC = DC$,将点$A$放在角的顶点,$AB和AD$沿着角的两边放下,沿$AC画一条射线AE$,$AE$就是这个角的平分线,请说明理由.
(2)操作:如图2,利用直尺和圆规作已知角平分线的作法如下:
①以点$O$为圆心,适当长为半径画弧,交$OA于点M$,交$OB于点N$.
②分别以点$M,N$为圆心,大于$\frac{1}{2}MN的长为半径画弧在\angle AOB的内部相交于点C$.
③画射线$OC$,射线$OC$即为所求.根据以上作法可知,$\triangle OMC\cong \triangle ONC$的依据是______SSS.
(3)应用:工人师傅常用角尺平分一个任意角,作法如下:如图3,$\angle AOB$是一个任意角,在边$AO,OB上分别取OM = ON$,移动角尺,使角尺两边相同的刻度分别与点$M,N$重合,过角尺顶点$C作射线OC$,求证:$\angle MCD= \angle NCD$.
(插图编号：1.3-13) (插图编号：1.3-14) (插图编号：1.3-15)

答案：
(1)解：在$\triangle ABC$和$\triangle ADC$中，$\begin{cases}AB = AD,\\BC = DC,\\AC = AC,\end{cases}$
$\therefore \triangle ABC\cong\triangle ADC(SSS).\therefore \angle BAC = \angle DAC$，
$\therefore AE$是$\angle BAD$的平分线.
(2)SSS
(3)证明：在$\triangle OMC$和$\triangle ONC$中，$\begin{cases}OM = ON,\\MC = NC,\\OC = OC,\end{cases}$
$\therefore \triangle OMC\cong\triangle ONC(SSS).\therefore \angle MCO = \angle NCO$.
$\because \angle MCO + \angle MCD = 180^{\circ},\angle NCO + \angle NCD = 180^{\circ},\therefore \angle MCD = \angle NCD$.