2025年暑假零距离七年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假零距离七年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
7. 如图,在$Rt△ABC$、$Rt△DEF$中,$∠B= ∠E= 90^{\circ }$,添加两个条件不能使这两个直角三角形全等的是 (
A.$∠A= ∠D,AB= DE$
B.$∠A= ∠D,BC= EF$
C.$AB= DE,BC= EF$
D.$∠A= ∠D,∠C= ∠F$
D
)A.$∠A= ∠D,AB= DE$
B.$∠A= ∠D,BC= EF$
C.$AB= DE,BC= EF$
D.$∠A= ∠D,∠C= ∠F$
答案:
D
8. 如图,在$△ABC$中,$AD⊥BC$于点D,要使$△ABD≌△ACD$,若根据“HL”判定,还需要加条件
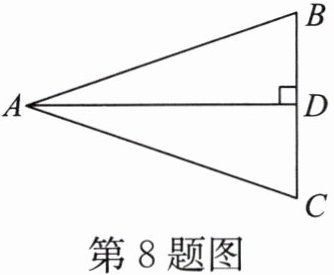
$ AB = AC $
.
答案:
$ AB = AC $
9. 如图,在$Rt△ABC与Rt△DEF$中,$∠B= ∠E= 90^{\circ },AC= DF,AB= DE,∠A= 50^{\circ }$,则$∠DFE= $
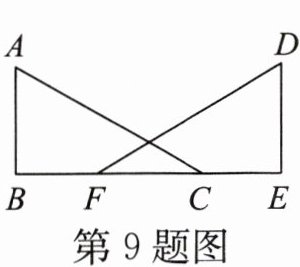
$40^{\circ}$
.
答案:
$ 40^{\circ} $
10. 如图,$MN// PQ,AB⊥PQ$,点A、D、B、C分别在直线MN与PQ上,点E在AB上,$AD+BC= 7,AD= EB,DE= EC$,则$AB= $
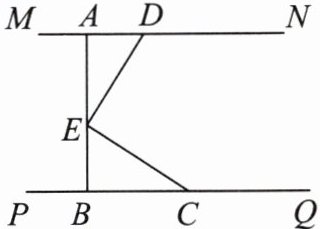
7
.
答案:
7
11. 如图,$∠A= ∠D= 90^{\circ },AB= DE,BF= EC$. 求证:$Rt△ABC≌Rt△DEF$.
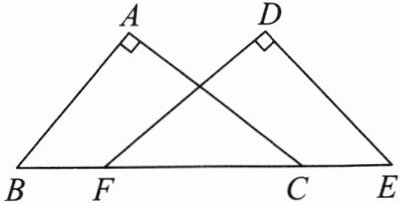

答案:
证明:$\because BF=EC$,
$\therefore BF+FC=FC+EC$,即$BC=EF$。
$\because \angle A=\angle D=90^{\circ }$,
$\therefore \triangle ABC$和$\triangle DEF$都是直角三角形。
在$Rt\triangle ABC$和$Rt\triangle DEF$中,
$\left\{\begin{array}{l} AB=DE,\\ BC=EF,\end{array}\right.$
$\therefore Rt\triangle ABC≌Rt\triangle DEF(HL)$。
$\therefore BF+FC=FC+EC$,即$BC=EF$。
$\because \angle A=\angle D=90^{\circ }$,
$\therefore \triangle ABC$和$\triangle DEF$都是直角三角形。
在$Rt\triangle ABC$和$Rt\triangle DEF$中,
$\left\{\begin{array}{l} AB=DE,\\ BC=EF,\end{array}\right.$
$\therefore Rt\triangle ABC≌Rt\triangle DEF(HL)$。
12. 在四边形ABCD中,$∠ABC= ∠ADC= 90^{\circ },BE⊥AC$于点E,$DF⊥AC$于点F,$CF= AE,BC= DA$. 求证:$Rt△ABE≌Rt△CDF$.


答案:
证明:$\because \angle ABC = \angle ADC = 90^{\circ}$,
$\therefore \triangle ADC$和$\triangle CBA$都是直角三角形。
在$Rt\triangle ADC$与$Rt\triangle CBA$中,
$\left\{ \begin{array}{l} DA = BC, \\ AC = CA, \end{array} \right.$
$\therefore Rt\triangle ADC \cong Rt\triangle CBA (HL)$,
$\therefore DC = BA$。
$\because BE \perp AC$,$DF \perp AC$,
$\therefore \angle AEB = \angle CFD = 90^{\circ}$。
在$Rt\triangle ABE$与$Rt\triangle CDF$中,
$\left\{ \begin{array}{l} AE = CF, \\ AB = CD, \end{array} \right.$
$\therefore Rt\triangle ABE \cong Rt\triangle CDF (HL)$。
$\therefore \triangle ADC$和$\triangle CBA$都是直角三角形。
在$Rt\triangle ADC$与$Rt\triangle CBA$中,
$\left\{ \begin{array}{l} DA = BC, \\ AC = CA, \end{array} \right.$
$\therefore Rt\triangle ADC \cong Rt\triangle CBA (HL)$,
$\therefore DC = BA$。
$\because BE \perp AC$,$DF \perp AC$,
$\therefore \angle AEB = \angle CFD = 90^{\circ}$。
在$Rt\triangle ABE$与$Rt\triangle CDF$中,
$\left\{ \begin{array}{l} AE = CF, \\ AB = CD, \end{array} \right.$
$\therefore Rt\triangle ABE \cong Rt\triangle CDF (HL)$。
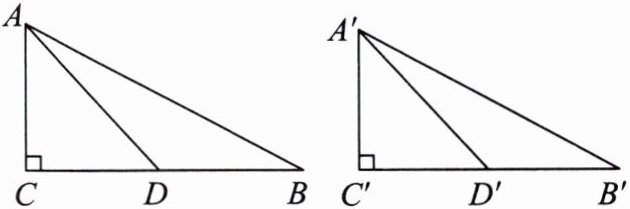
13. 如图,在$Rt△ABC和Rt△A'B'C'$中,$∠C= ∠C'= 90^{\circ },AC= A'C',AD与A'D'$分别为BC,$B'C'$边上的中线,且$AD= A'D'$,求证:$Rt△ABC≌Rt△A'B'C'$.

答案:
证明:在$Rt\triangle ACD$和$Rt\triangle A'C'D'$中,
$\left\{\begin{array}{l} AC=A'C'\\ AD=A'D'\end{array}\right.$
$\therefore Rt\triangle ACD≌Rt\triangle A'C'D'(HL)$
$\therefore CD=C'D'$
$\because AD$与$A'D'$分别为$BC$,$B'C'$边上的中线
$\therefore BC=2CD$,$B'C'=2C'D'$
$\therefore BC=B'C'$
在$Rt\triangle ABC$和$Rt\triangle A'B'C'$中,
$\left\{\begin{array}{l} AC=A'C'\\ \angle C=\angle C'=90^{\circ }\\ BC=B'C'\end{array}\right.$
$\therefore Rt\triangle ABC≌Rt\triangle A'B'C'(SAS)$
$\left\{\begin{array}{l} AC=A'C'\\ AD=A'D'\end{array}\right.$
$\therefore Rt\triangle ACD≌Rt\triangle A'C'D'(HL)$
$\therefore CD=C'D'$
$\because AD$与$A'D'$分别为$BC$,$B'C'$边上的中线
$\therefore BC=2CD$,$B'C'=2C'D'$
$\therefore BC=B'C'$
在$Rt\triangle ABC$和$Rt\triangle A'B'C'$中,
$\left\{\begin{array}{l} AC=A'C'\\ \angle C=\angle C'=90^{\circ }\\ BC=B'C'\end{array}\right.$
$\therefore Rt\triangle ABC≌Rt\triangle A'B'C'(SAS)$
查看更多完整答案,请扫码查看


