2025年暑假零距离七年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假零距离七年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
9. 如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP= 20°,∠ACP= 50°,则∠A+∠P=
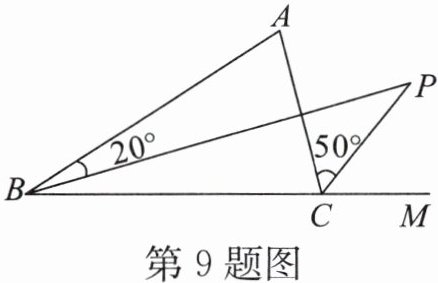
90°
.
答案:
$90^{\circ}$
10. 如图,在△ABC中,点O是三个角平分线的交点,∠BAO= 40°,则∠BOC= ______
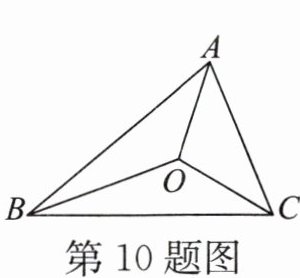
130°
.
答案:
$130^{\circ}$
11. 如图,在Rt△ABC中,∠ACB= 90°,直线a//b,∠1+∠B= 58°,则∠2=
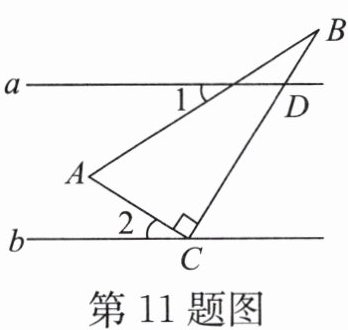
32°
.
答案:
$32^{\circ}$
12. 如图,在Rt△ABC中,∠ACB= 90°,∠B= 38°,将其折叠使点A落在BC边上的A'处,折痕为CD,则∠A'DB= ______

14°
.
答案:
$14^{\circ}$
13. 如图,在△ABC中,∠ABC= ∠C,∠ABC的角平分线与外角∠EAC的角平分线交于点D.
(1)求证:AD//BC;
(2)若∠BAC= 36°,求∠ADB的度数.
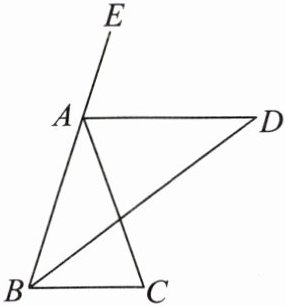
(1)求证:AD//BC;
(2)若∠BAC= 36°,求∠ADB的度数.

答案:
(1) 证明:$\because \angle ABC + \angle C + \angle BAC = 180^{\circ}$,$\angle CAD + \angle EAD + \angle BAC = 180^{\circ}$,$\therefore \angle ABC + \angle C = \angle CAD + \angle EAD$。$\because \angle ABC = \angle C$,$\angle CAD = \angle EAD$,$\therefore \angle C = \angle CAD$,$\therefore AD // BC$。
(2) 解:$\because \angle BAC = 36^{\circ}$,$\therefore \angle ABC = \angle C = \frac{1}{2}(180^{\circ} - \angle BAC) = 72^{\circ}$。$\because BD$平分$\angle ABC$,$\therefore \angle ABD = \angle CBD = \frac{1}{2}\angle ABC = 36^{\circ}$。$\because AD // BC$,$\therefore \angle ADB = \angle CBD = 36^{\circ}$。
(1) 证明:$\because \angle ABC + \angle C + \angle BAC = 180^{\circ}$,$\angle CAD + \angle EAD + \angle BAC = 180^{\circ}$,$\therefore \angle ABC + \angle C = \angle CAD + \angle EAD$。$\because \angle ABC = \angle C$,$\angle CAD = \angle EAD$,$\therefore \angle C = \angle CAD$,$\therefore AD // BC$。
(2) 解:$\because \angle BAC = 36^{\circ}$,$\therefore \angle ABC = \angle C = \frac{1}{2}(180^{\circ} - \angle BAC) = 72^{\circ}$。$\because BD$平分$\angle ABC$,$\therefore \angle ABD = \angle CBD = \frac{1}{2}\angle ABC = 36^{\circ}$。$\because AD // BC$,$\therefore \angle ADB = \angle CBD = 36^{\circ}$。
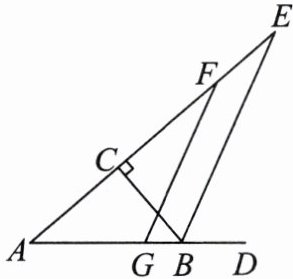
14. 如图,在Rt△ABC中,∠ACB= 90°,∠A= 40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)点G是AB上任意一点,过点G作GF//BE,交AC于点F,求∠AFG的度数.
(1)求∠CBE的度数;
(2)点G是AB上任意一点,过点G作GF//BE,交AC于点F,求∠AFG的度数.

答案:
解:
(1) $\because$在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$\angle A = 40^{\circ}$,$\therefore \angle ABC = 90^{\circ} - \angle A = 50^{\circ}$,$\therefore \angle CBD = 130^{\circ}$。$\because BE$是$\angle CBD$的平分线,$\therefore \angle CBE = \frac{1}{2}\angle CBD = 65^{\circ}$。
(2) $\because \angle ACB = 90^{\circ}$,$\angle CBE = 65^{\circ}$,$\therefore \angle CEB = 90^{\circ} - 65^{\circ} = 25^{\circ}$。$\because GF // BE$,$\therefore \angle AFG = \angle CEB = 25^{\circ}$。
(1) $\because$在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$\angle A = 40^{\circ}$,$\therefore \angle ABC = 90^{\circ} - \angle A = 50^{\circ}$,$\therefore \angle CBD = 130^{\circ}$。$\because BE$是$\angle CBD$的平分线,$\therefore \angle CBE = \frac{1}{2}\angle CBD = 65^{\circ}$。
(2) $\because \angle ACB = 90^{\circ}$,$\angle CBE = 65^{\circ}$,$\therefore \angle CEB = 90^{\circ} - 65^{\circ} = 25^{\circ}$。$\because GF // BE$,$\therefore \angle AFG = \angle CEB = 25^{\circ}$。
15. 如图,点D,E分别在△ABC的边AB,AC上,点F在线段CD上,且∠3= ∠B,DE//BC.
(1)求证:∠1+∠2= 180°;
(2)若DE平分∠ADC,∠2= 2∠B,求∠1的度数.

(1)求证:∠1+∠2= 180°;
(2)若DE平分∠ADC,∠2= 2∠B,求∠1的度数.

答案:
(1) 证明:$\because DE // BC$,$\therefore \angle ADE = \angle B$。$\because \angle 3 = \angle B$,$\therefore \angle 3 = \angle ADE$,$\therefore EF // AB$,$\therefore \angle 2 = \angle DFE$。$\because \angle 1 + \angle DFE = 180^{\circ}$,$\therefore \angle 1 + \angle 2 = 180^{\circ}$。
(2) 解:$\because DE$平分$\angle ADC$,$\therefore \angle ADC = 2\angle ADE$。$\because DE // BC$,$\therefore \angle ADE = \angle B$,$\therefore \angle ADC = 2\angle B$。$\because \angle 2 = 2\angle B$,$\angle 2 + \angle ADC = 180^{\circ}$,$\therefore 2\angle B + 2\angle B = 180^{\circ}$,解得$\angle B = 45^{\circ}$。由
(1)得$AB // EF$,$\therefore \angle 1 = \angle ADC = 2\angle B = 90^{\circ}$。
(1) 证明:$\because DE // BC$,$\therefore \angle ADE = \angle B$。$\because \angle 3 = \angle B$,$\therefore \angle 3 = \angle ADE$,$\therefore EF // AB$,$\therefore \angle 2 = \angle DFE$。$\because \angle 1 + \angle DFE = 180^{\circ}$,$\therefore \angle 1 + \angle 2 = 180^{\circ}$。
(2) 解:$\because DE$平分$\angle ADC$,$\therefore \angle ADC = 2\angle ADE$。$\because DE // BC$,$\therefore \angle ADE = \angle B$,$\therefore \angle ADC = 2\angle B$。$\because \angle 2 = 2\angle B$,$\angle 2 + \angle ADC = 180^{\circ}$,$\therefore 2\angle B + 2\angle B = 180^{\circ}$,解得$\angle B = 45^{\circ}$。由
(1)得$AB // EF$,$\therefore \angle 1 = \angle ADC = 2\angle B = 90^{\circ}$。
查看更多完整答案,请扫码查看


