《2025年暑假零距离七年级数学人教版》

9. 如图,点P在$∠AOB$的平分线上,则根据“SAS”判定$△AOP\cong △BOP$还需添加的条件是$ OA = OB $.

答案： $ OA = OB $

10. 如图,将两根钢条$AA',BB'$的中点O连在一起,使$AA',BB'$可以绕着点O自由转动,就做成了一个测量工具,则$A'B'$的长等于内槽宽AB,那么判定$△OAB\cong △OA'B'$的理由是SAS.

答案： SAS

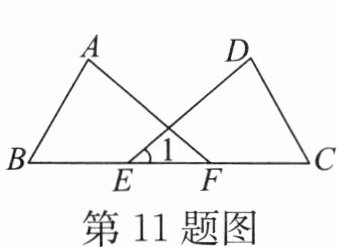
11. 如图,点E,F在BC上,$BE= CF,AB= DC,∠B= ∠C$,若$∠A= 80^{\circ },∠C= 60^{\circ }$,则$∠1= $$40^{\circ}$.

答案： $ 40^{\circ} $

12. 如图,AD与BC相交于点O,已知$OB= OC$,若以“SAS”为依据证明$△AOB\cong △DOC$,还需要添加的条件是$ OA = OD $.

答案： $ OA = OD $

13. 如图,在$△ABC和△AED$中,$AB= AE,∠BAE= ∠CAD,AC= AD$. 求证:$△ABC\cong △AED$.

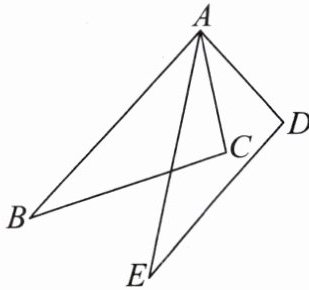
答案： 证明：$\because \angle BAE = \angle CAD$，
$\therefore \angle BAE + \angle CAE = \angle CAD + \angle CAE$，即$\angle BAC = \angle EAD$。
在$\triangle ABC$和$\triangle AED$中，
$\left\{\begin{array}{l} AB = AE,\\ \angle BAC = \angle EAD,\\ AC = AD,\end{array}\right.$
$\therefore \triangle ABC \cong \triangle AED(SAS)$。

14. 如图,点B,C,E,F共线,$AB= DC,∠B= ∠C,BF= CE$. 求证:$AE// DF$.

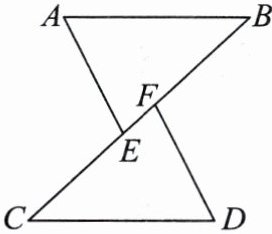
答案： 证明：$\because BF=CE$，
$\therefore BF+EF=CE+EF$，即$BE=CF$。
在$\triangle ABE$和$\triangle DCF$中，
$\left\{\begin{array}{l} AB=DC,\\ \angle B=\angle C,\\ BE=CF,\end{array}\right.$
$\therefore \triangle ABE \cong \triangle DCF(\text{SAS})$。
$\therefore \angle AEB=\angle DFC$，
$\therefore AE // DF$。

15. 如图,在$△ADC$中,DB是高,点E是DB上一点,$AB= DB,EB= CB$,M,N分别是AE,CD上的点,且$AM= DN$.
(1)求证:$△ABE\cong △DBC$.
(2)求证:$BM= BN$.

答案： 证明：
(1)$\because DB$是 $ △ADC $的高，$\therefore ∠ABE = ∠DBC = 90^{\circ}$。在 $ △ABE $和 $ △DBC $中，$\left\{\begin{array}{l} AB = DB,\\ ∠ABE = ∠DBC,\\ EB = CB,\end{array}\right. $ $\therefore △ABE ≌ △DBC(SAS)$。
(2)由
(1)知 $ △ABE ≌ △DBC $，$\therefore ∠BAM = ∠BDN$。在 $ △ABM $和 $ △DBN $中，$\left\{\begin{array}{l} AB = DB,\\ ∠BAM = ∠BDN,\\ AM = DN,\end{array}\right. $ $\therefore △ABM ≌ △DBN(SAS)$。$\therefore BM = BN$。