2025年暑假零距离七年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假零距离七年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
6. 如图,在$△ABC$中,$∠ACB = 90^{\circ}$,$BE平分∠ABC$,$DE⊥AB于点D$。若$AC = 5cm$,则$AE + DE = $(
A.$2cm$
B.$3cm$
C.$4cm$
D.$5cm$
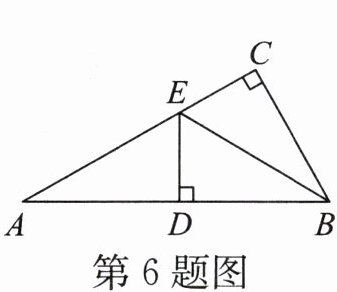
D
)A.$2cm$
B.$3cm$
C.$4cm$
D.$5cm$

答案:
D
7. 如图,$BO平分∠ABC$,$OD⊥BC于点D$,点$E为射线BA$上一动点,若$OD = 3$,则$OE$的最小值为____

3
。
答案:
3
8. 如图,在$△ABC$中,$AD平分∠BAC$,$AB = 8$,$AC = 6$,则$S_{△ABD}:S_{△ACD}= $

$4:3$
。
答案:
$4:3$
9. 如图,在$Rt△ABC$中,$∠C = 90^{\circ}$,$BD是∠ABC$的平分线,$DE⊥AB$,垂足为$E$。若$AC = 5$,$DE = 2$,则$AD$的长为____
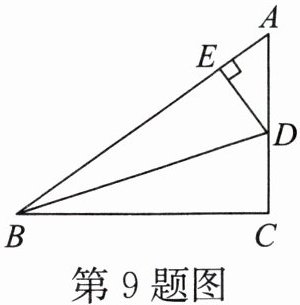
3
。
答案:
3
10. 如图,$BD平分∠ABC$,$AB = BC$,点$P在BD$上,$PM⊥AD$,$PN⊥CD$,$M$,$N$为垂足。求证:$PM = PN$。


答案:
证明:在$\triangle ABD$和$\triangle CBD$中,
$\left\{\begin{array}{l} AB=CB,\\ ∠ABD=∠CBD,\\ BD=BD,\end{array}\right.$
$\therefore \triangle ABD\cong \triangle CBD(SAS)$,
$\therefore ∠ADB=∠CDB$.
$\because PM⊥AD$,$PN⊥CD$,
$\therefore PM=PN$.
$\left\{\begin{array}{l} AB=CB,\\ ∠ABD=∠CBD,\\ BD=BD,\end{array}\right.$
$\therefore \triangle ABD\cong \triangle CBD(SAS)$,
$\therefore ∠ADB=∠CDB$.
$\because PM⊥AD$,$PN⊥CD$,
$\therefore PM=PN$.
11. 已知,在$Rt△ABC$中,$∠C = 90^{\circ}$,$AD是∠BAC$的平分线。若$AC = 6$,$BC = 8$,$AB = 10$,请求出$CD$的长度。


答案:
解:过点D作DE⊥AB于点E。
∵AD平分∠BAC,∠C=90°,DE⊥AB,
∴DE=CD(角平分线上的点到角两边的距离相等)。
∵S△ABC=S△ACD+S△ABD,
∴$\frac{1}{2}×AC×BC=\frac{1}{2}×AC×CD+\frac{1}{2}×AB×DE$。
∵AC=6,BC=8,AB=10,DE=CD,
∴$\frac{1}{2}×6×8=\frac{1}{2}×6×CD+\frac{1}{2}×10×CD$,
即24=3CD+5CD,
8CD=24,
解得CD=3。
答:CD的长度为3。
∵AD平分∠BAC,∠C=90°,DE⊥AB,
∴DE=CD(角平分线上的点到角两边的距离相等)。
∵S△ABC=S△ACD+S△ABD,
∴$\frac{1}{2}×AC×BC=\frac{1}{2}×AC×CD+\frac{1}{2}×AB×DE$。
∵AC=6,BC=8,AB=10,DE=CD,
∴$\frac{1}{2}×6×8=\frac{1}{2}×6×CD+\frac{1}{2}×10×CD$,
即24=3CD+5CD,
8CD=24,
解得CD=3。
答:CD的长度为3。
12. 如图,$C是∠MAN$的角平分线上一点,$CE⊥AN$,$CF⊥AM$,垂足分别为$E$,$F$。过点$C作CD// AN$,交$AM于点D$,在射线$EN上取一点B$,使$∠CBE = 2∠DCA$。
(1)求证:$CF = CE$;
(2)求证:$DF = BE$。
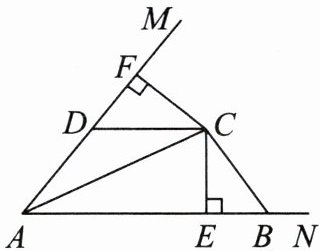
(1)求证:$CF = CE$;
(2)求证:$DF = BE$。

答案:
证明:
(1)$\because AC$是$∠MAN$角平分线,$\therefore ∠MAC=∠NAC.\because CE⊥AN,CF⊥AM,\therefore ∠CFA=∠CEA=90^{\circ }$. 在$\triangle CAF$与$\triangle CAE$中,$\left\{\begin{array}{l} ∠MAC=∠NAC,\\ ∠CFA=∠CEA,\\ AC=AC,\end{array}\right. $$\therefore \triangle CAF\cong \triangle CAE(AAS),\therefore CF=CE$.
(2)由
(1)知$CF=CE.\because CD// AN,\therefore ∠FDC=∠DAE,\therefore ∠DCA=∠CAE=\frac{1}{2}DAE.\because ∠CBE=2∠DCA,\therefore ∠CBE=∠DAE,\therefore ∠CBE=∠FDC$.在$\triangle CFD$和$\triangle CEB$中,$\left\{\begin{array}{l} ∠CDF=∠CBE,\\ ∠CFD=∠CEB=90^{\circ },\\ CF=CE,\end{array}\right. $$\therefore \triangle CFD\cong \triangle CEB(AAS),\therefore DF=BE$.
(1)$\because AC$是$∠MAN$角平分线,$\therefore ∠MAC=∠NAC.\because CE⊥AN,CF⊥AM,\therefore ∠CFA=∠CEA=90^{\circ }$. 在$\triangle CAF$与$\triangle CAE$中,$\left\{\begin{array}{l} ∠MAC=∠NAC,\\ ∠CFA=∠CEA,\\ AC=AC,\end{array}\right. $$\therefore \triangle CAF\cong \triangle CAE(AAS),\therefore CF=CE$.
(2)由
(1)知$CF=CE.\because CD// AN,\therefore ∠FDC=∠DAE,\therefore ∠DCA=∠CAE=\frac{1}{2}DAE.\because ∠CBE=2∠DCA,\therefore ∠CBE=∠DAE,\therefore ∠CBE=∠FDC$.在$\triangle CFD$和$\triangle CEB$中,$\left\{\begin{array}{l} ∠CDF=∠CBE,\\ ∠CFD=∠CEB=90^{\circ },\\ CF=CE,\end{array}\right. $$\therefore \triangle CFD\cong \triangle CEB(AAS),\therefore DF=BE$.
查看更多完整答案,请扫码查看


