《2025年暑假零距离七年级数学人教版》

10. 将命题“在同一平面内,垂直于同一条直线的两条直线互相平行”改写为“如果……那么……”的形式,可写为同一平面内，如果两条直线垂直于同一条直线，那么这两条直线互相平行.

答案： 同一平面内，如果两条直线垂直于同一条直线，那么这两条直线互相平行

11. 能说明命题:“若两个角$α,β$互补,则这两个角必为一个锐角一个钝角”是假命题的反例是$\alpha = 90^{\circ}$，$\beta = 90^{\circ}$.

答案： $\alpha = 90^{\circ}$，$\beta = 90^{\circ}$

12. 如图,直线$a,b被直线c$所截,请添加一个条件:$\angle 1 = \angle 3$（答案不唯一）,使得$a// b$.(只写一种情况即可)

答案： $\angle 1 = \angle 3$（答案不唯一）

13. 如图,直线$AB,CD相交于点O$,$OE把∠BOD$分成两部分,若$∠AOC= 70^{\circ }$,且$∠BOE:∠EOD= 2:3$,则$∠AOE$的度数为$152^{\circ}$.

答案： $152^{\circ}$

14. 如图,$∠1= 133^{\circ },AO⊥OB于点O$,点$C$,$O$,$D$在一条直线上,则$∠2= $______43$^{\circ }$.

答案： 43

15. 如图,已知直线$a// b$,直线$m⊥n$,垂足$O在直线b$上.若$∠1= 115^{\circ }$,则$∠2$的度数为______25°.

答案： $25^{\circ}$

16. 如图,将两个含$30^{\circ }$角的直角三角板的最长边靠在一起滑动,可知直角边$AB// CD$,依据是内错角相等，两直线平行.

答案： 内错角相等，两直线平行

17. 如图,在边长为1的正方形网格中,三角形$ABC和三角形A'B'C'$的顶点都在格点上,且三角形$A'B'C'是由三角形ABC向右平移M$个单位,再向上平移$N$个单位得到的,则$M+N$的值为5.

答案： 5

18. (8分)如图,直线$AB与CD相交于点O$,$OC平分∠AOM$,且$∠AOM= 90^{\circ }$,射线$ON在∠BOM$内部.
(1)求$∠AOD$的度数;
(2)若$∠BOC= 5∠NOB$,求$∠MON$的度数.

答案： 解:
(1) $\because \angle AOM = 90^{\circ}$，$OC$ 平分 $\angle AOM$，
$\therefore \angle AOC = \frac{1}{2}\angle AOM = \frac{1}{2} × 90^{\circ} = 45^{\circ}$。$\because \angle AOC + \angle AOD = 180^{\circ}$，$\therefore \angle AOD = 180^{\circ} - \angle AOC = 180^{\circ} - 45^{\circ} = 135^{\circ}$。
(2) $\because \angle BOC = \angle AOD = 135^{\circ}$，$\angle BOC = 5\angle NOB$，
$\therefore \angle NOB = 27^{\circ}$。$\because \angle AOM = 90^{\circ}$，$\therefore \angle BOM = 90^{\circ}$，
$\therefore \angle MON = \angle BOM - \angle NOB = 90^{\circ} - 27^{\circ} = 63^{\circ}$。

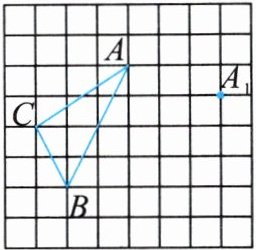
19. (9分)如图,三角形$ABC$的三个顶点都在正方形网格的格点上(网格中每个小正方形的边长都为1个单位长度),将三角形$ABC$平移,使点$A平移到A_{1}$的位置.
(1)画出平移后的三角形$A_{1}B_{1}C_{1}$;
(2)连接$AA_{1},BB_{1}$,则线段$AA_{1}与BB_{1}$的位置关系是______;
(3)求线段$AC$在平移的过程中扫过的图形面积.

答案：
解:
(1)如图,三角形 $A_1B_1C_1$ 即为所求。
(2) 平行
(3)如图,连接 $CC_1$，四边形 $AA_1C_1C$ 的面积为 $6 × 3 - 2 × \frac{1}{2} × 3 × 2 - 2 × \frac{1}{2} × 3 × 1 = 9$。