《2025年暑假零距离七年级数学人教版》

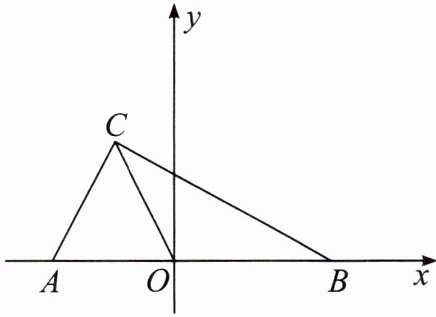
17. (12分)如图,在平面直角坐标系中,已知$A(a,0),B(b,0),C(-1,2)$,且$|a+2|+(b-3)^{2}= 0$.
(1)求a,b的值;
(2)①在y轴的正半轴上存在一点M,使$S_{三角形COM}= \frac {1}{2}S_{三角形ABC}$,求点M的坐标;
②在坐标轴的其他位置是否存在点M,使$S_{三角形COM}= \frac {1}{2}S_{三角形ABC}$仍然成立?若存在,请直接写出符合条件的点M的坐标.

答案： 解：
(1)$\because |a + 2| + (b - 3)^2 = 0$，$\therefore a = -2$，$b = 3$。
(2)①设$M(0,m)$。由题意，得$\frac{1}{2}m×1 = \frac{1}{2}×\frac{1}{2}×(2 + 3)×2$，解得$m = 5$，$\therefore M(0,5)$。
②当$M$在$y$轴的负半轴上时，$\frac{1}{2}(-m)×1 = \frac{1}{2}×\frac{1}{2}×(2 + 3)×2$，解得$m = -5$，$\therefore M(0,-5)$；当$M$在$x$轴上时，设$M(n,0)$，则$\frac{1}{2}×|n|×2 = \frac{1}{2}×\frac{1}{2}×(2 + 3)×2$，解得$n = ±\frac{5}{2}$，$\therefore M(±\frac{5}{2},0)$。
故符合条件的点$M$的坐标为$(\frac{5}{2},0)$或$(-\frac{5}{2},0)$或$(0,-5)$。

18. (12分)在平面直角坐标系中,对于点$A(x,y)$,若点B的坐标为$(kx+y,x-ky)$,则称点B为点A的“k级关联点”,如点$A(2,5)$的“2级关联点”点B的坐标为$(2×2+5,2-2×5)$,即$B(9,-8)$.
(1)已知点$P(-4,2)$的“-3级关联点”为$P_{1}$,求点$P_{1}$的坐标,并写出点$P_{1}$到y轴的距离;
(2)已知点Q的“4级关联点”为$Q_{1}(-11,10)$,求Q点的坐标及所在象限;
(3)如果点$M(a,a+2)$的“2级关联点”$M_{1}$在x轴上,求点$M_{1}$的坐标.

答案： 解：
(1)$\because$点$P(-4,2)$的“$-3$级关联点”的横坐标为$-3×(-4) + 2 = 14$，纵坐标为$-4 - (-3)×2 = 2$，$\therefore$点$P_1$的坐标为$(14,2)$，点$P_1$到$y$轴的距离为$14$。
(2)设$Q$点的坐标为$(a,b)$，$\because$点$Q$的“$4$级关联点”为$Q_1(-11,10)$，$\therefore 4a + b = -11$，$a - 4b = 10$，解得$a = -2$，$b = -3$，$\therefore Q$点的坐标为$(-2,-3)$，$Q$点所在的象限为第三象限。
(3)设点$M_1$的坐标为$(m,0)$，$\because$点$M(a,a + 2)$的“$2$级关联点”为$M_1$，$\therefore a - 2(a + 2) = 0$，$\therefore a = -4$，$\therefore a + 2 = -2$，$\therefore m = 2×(-4) + (-2) = -10$，$\therefore$点$M_1$的坐标为$(-10,0)$。

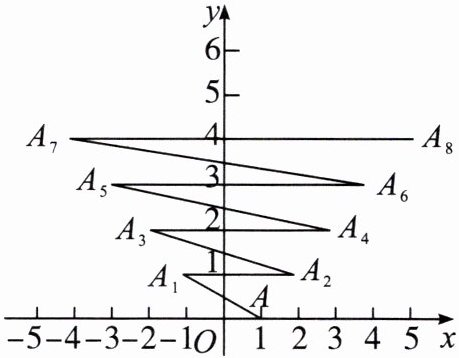
19. (14分)如图,在平面直角坐标系中,已知点A的坐标是$(1,0)$,点A第一次跳动至点$A_{1}(-1,1)$,第二次向右跳动3个单位长度至点$A_{2}(2,1)$,第三次跳动至点$A_{3}(-2,2)$,第四次向右跳动5个单位长度至点$A_{4}(3,2),...$,以此规律跳动下去.
(1)求$A_{1001}$到x轴的距离;
(2)若从$A_{1001}跳动到A_{1002},A_{1001}A_{1002}$长为多少? 写出$A_{1002}$的坐标.

答案： 解：
(1)点的坐标依次为$A_1(-1,1)$，$A_2(2,1)$，$A_3(-2,2)$，$A_4(3,2)$，$A_5(-3,3)$，$A_6(4,3)$，$A_7(-4,4)$，$A_8(5,4)$，$\cdots$，$A_{2n - 1}(-n,n)$，$A_{2n}(n + 1,n)$（$n$为整数），$\therefore 2n - 1 = 1001$，$n = 501$，$\therefore A_{1001}(-501,501)$，即点$A_{1001}$到$x$轴的距离为$501$。
(2)若从$A_{1001}$跳动到$A_{1002}$是向右跳动了$1003$个单位长度，则$A_{1001}A_{1002} = 1003$，点$A_{1002}$的坐标是$(502,501)$。