《2025年快乐暑假天天练七年级数学生物》

1.已知a＜b,则下列不等式一定成立的是()
A. ca＞cb
B. -a＜-b
C. a-b＜0
D. a+3＞b+3

答案： 1. 对于选项A：
- 根据不等式的基本性质，不等式两边同时乘（或除以）同一个正数，不等号的方向不变；不等式两边同时乘（或除以）同一个负数，不等号的方向改变。
- 当$c\gt0$时，$ca\lt cb$；当$c = 0$时，$ca=cb$；当$c\lt0$时，$ca\gt cb$，所以选项A不一定成立。
2. 对于选项B：
- 根据不等式的基本性质，不等式两边同时乘（或除以）同一个负数，不等号的方向改变。
- 因为$a\lt b$，两边同时乘以$-1$，得到$-a\gt -b$，所以选项B不成立。
3. 对于选项C：
- 因为$a\lt b$，在不等式两边同时减去$b$，根据不等式的基本性质，不等式两边同时加上或减去同一个整式，不等号方向不变，所以$a - b\lt b - b$，即$a - b\lt0$，选项C一定成立。
4. 对于选项D：
- 因为$a\lt b$，在不等式两边同时加上$3$，根据不等式的基本性质，不等式两边同时加上或减去同一个整式，不等号方向不变，所以$a + 3\lt b + 3$，选项D不成立。
C

2.若(m+1)x$^{\mid m+2\mid}$+4＜0是关于x的一元一次不等式,则m的值为()
A. -1
B. -3
C. -2
D. -3或-1

答案： 由$\vert m + 2\vert = 1$可得$m + 2 = 1$或$m + 2 = -1$。
当$m + 2 = 1$时，$m = 1 - 2 = -1$；当$m + 2 = -1$时，$m = -1 - 2 = -3$。
又因为$m + 1\neq 0$，即$m\neq -1$，所以$m = -3$。
B

3.如图是两位同学在讨论一个一元一次不等式,根据对话中提供的信息判断,他们讨论的不等式可能是()

A. 2x＜6
B. -2x＞-6
C. -x≤3
D. -2x≥-6

答案： 选项A：解不等式$2x\lt6$，两边同时除以$2$，根据不等式的基本性质$2$（不等式两边同时乘（或除以）同一个正数，不等号的方向不变），得$x\lt3$，此过程不需要改变不等号方向，不符合要求。
- 选项B：解不等式$-2x\gt - 6$，两边同时除以$-2$，根据不等式的基本性质$3$（不等式两边同时乘（或除以）同一个负数，不等号的方向改变），得$x\lt3$，此过程改变了不等号方向，且解集为$x\lt3$，符合要求。
- 选项C：解不等式$-x\leqslant3$，两边同时除以$-1$，根据不等式的基本性质$3$，得$x\geqslant - 3$，解集不符合要求。
- 选项D：解不等式$-2x\geqslant - 6$，两边同时除以$-2$，根据不等式的基本性质$3$，得$x\leqslant3$，解集是$x\leqslant3$（包含$3$这个点，是实心点），而图中是空心点，不符合要求。
B

4.在下列数轴上,不等式组$\begin{cases}1-2x＜3,\\3(x-1)\leq2x-1\end{cases}$的解集表示正确的是()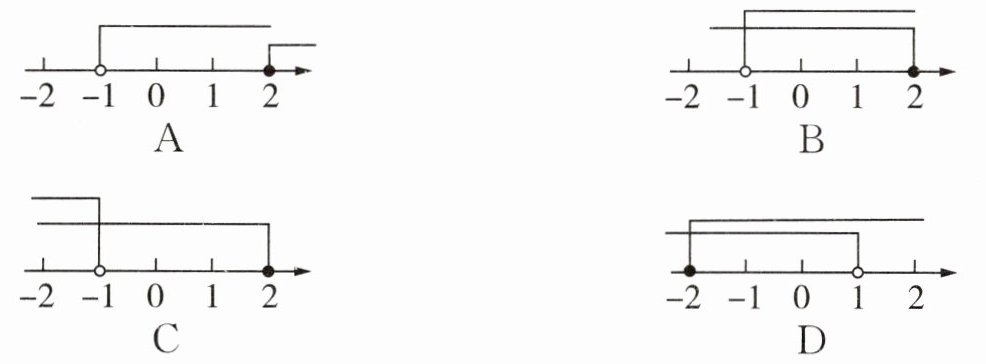

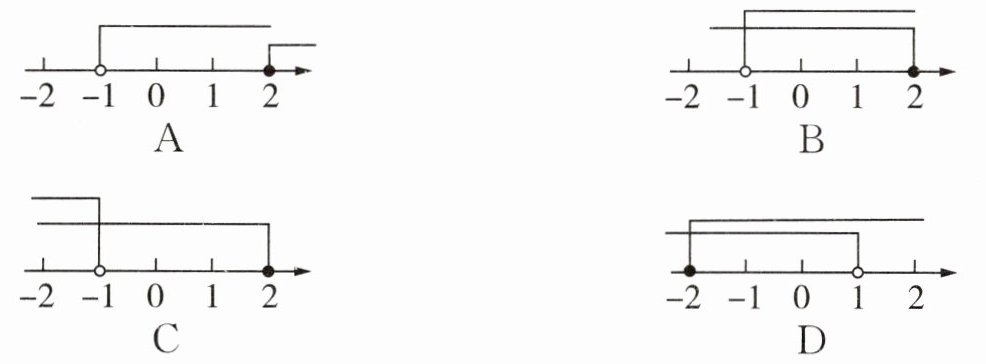
答案： 本题可先分别求解不等式组中的两个不等式，再取其交集得到不等式组的解集，最后根据解集判断数轴表示是否正确。
**步骤一：求解不等式$1 - 2x \lt 3$。**
对不等式$1 - 2x \lt 3$进行移项可得：$-2x\lt 3 - 1$，即$-2x\lt 2$。
不等式两边同时除以$-2$，根据不等式两边同时除以一个负数，不等号方向改变，可得$x\gt -1$。
**步骤二：求解不等式$3(x - 1) \leq 2x - 1$。**
先去括号：$3x - 3 \leq 2x - 1$。
再移项：$3x - 2x \leq -1 + 3$。
合并同类项可得$x \leq 2$。
**步骤三：求不等式组的解集。**
综合两个不等式的解$x\gt -1$和$x \leq 2$，根据“大小小大中间找”的原则，可得不等式组的解集为$-1\lt x\leq 2$。
**步骤四：根据解集判断数轴表示。**
在数轴上表示不等式的解集时，大于号向右画，小于等于号向左画，空心圆圈表示不包含该点，实心圆点表示包含该点。
- 选项A：表示的解集是$x\gt -1$与$x\geq 2$的并集，不符合要求。
- 选项B：表示的解集是$-1\lt x\leq 2$，符合要求。
- 选项C：表示的解集是$x\lt -1$与$x\leq 2$的交集，不符合要求。
- 选项D：表示的解集是$-2\leq x\lt 1$，不符合要求。
$\boldsymbol{B}$