《2025年快乐暑假天天练七年级数学生物》

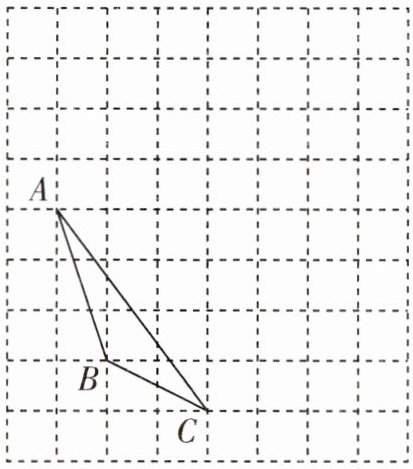
1. 如图,在$9× 8$的正方形网格中,每个小正方形的顶点称为格点,每个小正方形的边长均为$1$,点$A$,$B$,$C$均在格点上,请只用无刻度的直尺,在给定的网格中按要求作图并回答(3)中问题。
(1)将$\triangle ABC向右平移3$个单位长度,得到$\triangle A_1B_1C_1$；
(2)将$\triangle ABC绕点A逆时针旋转90^{\circ}$,得到$\triangle AB_2C_2$；
(3)图中$AC_2与A_1C_1$的位置关系为______。

答案：
(1) 平移的性质是图形平移后，对应点所连的线段平行且相等，对应线段平行且相等。将点$A$、$B$、$C$分别向右平移$3$个单位长度，得到$A_1$、$B_1$、$C_1$，然后连接$A_1B_1$、$B_1C_1$、$A_1C_1$，得到$\triangle A_1B_1C_1$。
(2) 旋转的性质是图形旋转后，对应点到旋转中心的距离相等，对应线段的长度相等，对应角的大小相等。将点$B$、$C$绕点$A$逆时针旋转$90^{\circ}$，得到$B_2$、$C_2$，然后连接$AB_2$、$AC_2$、$B_2C_2$，得到$\triangle AB_2C_2$。
(3) 可通过观察图形或证明来判断$AC_2$与$A_1C_1$的位置关系。
- 方法一（观察法）：通过作图后直观观察可得$AC_2$与$A_1C_1$的位置关系。
- 方法二（证明法）：
- 设网格中横向相邻格点距离为$a = 1$，纵向相邻格点距离为$b = 1$。
- 根据勾股定理，$AC=\sqrt{(3a)^2+(2b)^2}=\sqrt{9 + 4}=\sqrt{13}$，$AC_2=\sqrt{(3a)^2+(2b)^2}=\sqrt{13}$，$A_1C_1=\sqrt{(3a)^2+(2b)^2}=\sqrt{13}$。
- 再计算$AA_1 = 3$，$C_1C_2=3$。
- 因为$\triangle AA_1C_1$和$\triangle AC_2C_1$中，$AA_1 = C_1C_2$，$AC_2 = A_1C_1$，$A_1C_1=A_1C_1$（公共边），所以$\triangle AA_1C_1\cong\triangle C_2C_1A$（$SSS$）。
- 则$\angle AA_1C_1+\angle C_1A_1C_2+\angle C_2A_1C=\angle C_2C_1A+\angle C_1A_1C_2+\angle C_2A_1C = 180^{\circ}$，且$\angle AA_1C_1=\angle C_2C_1A$，所以$AC_2// A_1C_1$。
(1) 按平移性质作出$\triangle A_1B_1C_1$（图略）。
(2) 按旋转性质作出$\triangle AB_2C_2$（图略）。
(3) 平行。

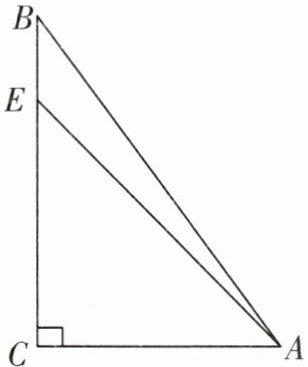
2. 如图,在$\triangle ABC$中,$\angle C = 90^{\circ}$,$a$,$b$,$c分别是\angle A$,$\angle B$,$\angle C$的对边,点$E是BC$上一个动点(点$E与点B$、点$C$不重合),连结$AE$。已知$a$,$b满足\begin{cases}b - 6 = 0,\\2a - b = 10,\end{cases}且c是不等式组\begin{cases}\dfrac{x + 12}{4}\leqslant x + 6,\\\dfrac{2x + 2}{3}＞x - 3\end{cases}$的最大整数解。
(1)求$a$,$b$,$c$的值；
(2)若$AE平分\triangle ABC$的周长,求$\angle AEC$的大小。

答案： $(1)$求$a$，$b$，$c$的值
- 求解$a$，$b$的值：
已知$\begin{cases}b - 6 = 0\\2a - b = 10\end{cases}$，
由$b - 6 = 0$，可得$b = 6$。
把$b = 6$代入$2a - b = 10$，即$2a-6 = 10$，
移项可得$2a=10 + 6$，
即$2a=16$，解得$a = 8$。
- 求解$c$的值：
解不等式组$\begin{cases}\dfrac{x + 12}{4}\leqslant x + 6\\\dfrac{2x + 2}{3}\gt x - 3\end{cases}$
- 解不等式$\dfrac{x + 12}{4}\leqslant x + 6$：
不等式两边同时乘以$4$得$x + 12\leqslant 4(x + 6)$，
去括号得$x + 12\leqslant 4x+24$，
移项得$x-4x\leqslant 24 - 12$，
合并同类项得$-3x\leqslant 12$，
解得$x\geqslant - 4$。
- 解不等式$\dfrac{2x + 2}{3}\gt x - 3$：
不等式两边同时乘以$3$得$2x + 2\gt 3(x - 3)$，
去括号得$2x + 2\gt 3x-9$，
移项得$2x-3x\gt -9 - 2$，
合并同类项得$-x\gt -11$，
解得$x\lt 11$。
所以不等式组的解集为$-4\leqslant x\lt 11$，则其最大整数解$c = 10$。
$(2)$求$\angle AEC$的大小
已知$a = 8$，$b = 6$，$c = 10$，$\triangle ABC$的周长为$a + b + c=8 + 6 + 10 = 24$。
因为$AE$平分$\triangle ABC$的周长，所以$BE + AB=EC + AC=\dfrac{1}{2}\times24 = 12$。
又因为$AB = c = 10$，$AC = b = 6$，所以$BE=12 - 10 = 2$，$EC=8 - 2 = 6$。
因为$AC = 6$，所以$EC = AC$。
在$Rt\triangle ABC$中，$\angle C = 90^{\circ}$，$EC = AC$，所以$\angle AEC=\angle EAC = 45^{\circ}$。
$(1)$解方程组$\begin{cases}b - 6 = 0\\2a - b = 10\end{cases}$得$\begin{cases}b = 6\\a = 8\end{cases}$；
解不等式组$\begin{cases}\dfrac{x + 12}{4}\leqslant x + 6\\\dfrac{2x + 2}{3}\gt x - 3\end{cases}$得$-4\leqslant x\lt 11$，$c = 10$。
所以$a = 8$，$b = 6$，$c = 10$。
$(2)$因为$AE$平分$\triangle ABC$周长，$\triangle ABC$周长为$24$，所以$BE + AB=EC + AC = 12$，
又$AB = 10$，$AC = 6$，所以$BE = 2$，$EC = 6$，
因为$EC = AC = 6$，$\angle C = 90^{\circ}$，所以$\angle AEC = 45^{\circ}$。
综上，$(1)$$\boldsymbol{a = 8}$，$\boldsymbol{b = 6}$，$\boldsymbol{c = 10}$；$(2)$$\boldsymbol{\angle AEC = 45^{\circ}}$。