《2025年快乐暑假天天练七年级数学生物》

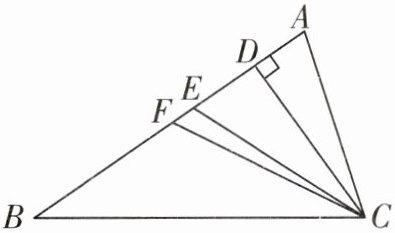
1. 如图,CD,CE,CF分别是△ABC的高、角平分线、中线,则下列各式中错误的是()

A. $ AB = 2BF $
B. $ AE = BE $
C. $ ∠ACE = \frac{1}{2}∠ACB $
D. $ CD⊥AB $

答案： 选项A：因为CF是$\triangle ABC$的中线，根据中线的定义，中线是连接三角形一个顶点和它所对边的中点的线段，所以$AB = 2BF$，该选项**正确**。
选项B：CE是$\triangle ABC$的角平分线，角平分线是将一个角平均分成两个相等角的射线，而不是平分对边，所以$AE\neq BE$，该选项**错误**。
选项C：由于CE是$\triangle ABC$的角平分线，根据角平分线的性质，$\angle ACE=\frac{1}{2}\angle ACB$，该选项**正确**。
选项D：因为CD是$\triangle ABC$的高，根据高的定义，从三角形的一个顶点向它的对边所在直线作垂线，顶点和垂足之间的线段叫做三角形的高，所以$CD\perp AB$，该选项**正确**。
B

2. 把一根18cm的铁丝按下面选项中的长度剪开,剪成的三段拉直后首尾顺次相接可以围成三角形的是()
A. 10cm,5cm,3cm
B. 9cm,5cm,4cm
C. 11cm,4cm,3cm
D. 7cm,7cm,4cm

答案： 选项A：$3 + 5 = 8\lt10$，不满足两边之和大于第三边，所以不能围成三角形。
选项B：$4 + 5 = 9$，不满足两边之和大于第三边，所以不能围成三角形。
选项C：$3 + 4 = 7\lt11$，不满足两边之和大于第三边，所以不能围成三角形。
选项D：$4 + 7 = 11\gt7$，$7 + 7 = 14\gt4$，满足两边之和大于第三边；$7 - 4 = 3\lt7$，$7 - 7 = 0\lt4$，满足两边之差小于第三边，所以能围成三角形。
D

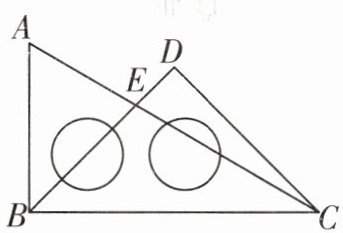
3. 如图是一副三角尺拼成的图案,则$ ∠AED $的度数为()

A. $ 95^{\circ} $
B. $ 100^{\circ} $
C. $ 105^{\circ} $
D. $ 110^{\circ} $

答案： **步骤一：求出$\angle ACB$与$\angle DBC$的度数**
已知该图是由一副三角尺拼成的图案，其中$\triangle ABC$是等腰直角三角形，$\angle ABC = 90^{\circ}$，$\angle A=\angle ACB = 45^{\circ}$；$\triangle DBC$是直角三角形，$\angle D = 90^{\circ}$，$\angle DCB = 30^{\circ}$，所以$\angle DBC = 60^{\circ}$。
**步骤二：求出$\angle ADB$的度数**
因为$\angle DBC$与$\angle ADB$是内错角，且$AD// BC$（三角尺的特性），根据“两直线平行，内错角相等”，可得$\angle ADB=\angle DBC = 60^{\circ}$。
**步骤三：求出$\angle AED$的度数**
在$\triangle ADE$中，$\angle AED$是外角，根据三角形外角的性质“三角形的一个外角等于与它不相邻的两个内角之和”，可得$\angle AED=\angle A+\angle ADB$。
已知$\angle A = 45^{\circ}$，$\angle ADB = 60^{\circ}$，所以$\angle AED=45^{\circ}+60^{\circ}=105^{\circ}$。
C

4. 若一个多边形的外角和是它的内角和的2倍,则这个多边形是()
A. 三角形
B. 四边形
C. 五边形
D. 六边形

答案： $\begin{aligned}360^{\circ}&=2\times(n - 2)\times180^{\circ}\\1&=(n - 2)\\n&=3\end{aligned}$
所以这个多边形是三角形。
A

5. 过七边形的一个顶点可以画n条对角线,将它分成m个三角形,则$ m + n $的值是()
A. 7
B. 8
C. 9
D. 10

答案： C