《2025年快乐暑假天天练七年级数学生物》

5. 关于x,y的方程组$ \left\{ \begin{array} { l } { 2 x + 3 y = 19, } \\ { a x + b y = - 1 } \end{array} \right. 与 \left\{ \begin{array} { l } { 3 x - 2 y = 9, } \\ { b x + a y = - 7 } \end{array} \right. $有相同的解,则$ a + 4 b - 5 $的值为()
A. -1
B. -6
C. -10
D. -12

答案： 给$2x + 3y = 19$两边同时乘以$2$得$4x + 6y = 38$，
给$3x - 2y = 9$两边同时乘以$3$得$9x - 6y = 27$，
将上述两个新方程相加可得：$4x + 6y+9x - 6y = 38 + 27$，
即$13x = 65$，解得$x = 5$。
把$x = 5$代入$2x + 3y = 19$，得$2\times5 + 3y = 19$，
即$10 + 3y = 19$，$3y = 9$，解得$y = 3$。
把$x = 5$，$y = 3$代入$\begin{cases}ax + by = -1 \\bx + ay = -7 \end{cases}$，得到$\begin{cases}5a + 3b = -1 \\5b + 3a = -7 \end{cases}$，
将$5a + 3b = -1$两边同时乘以$5$得$25a + 15b = -5$，
将$5b + 3a = -7$两边同时乘以$3$得$15b + 9a = -21$，
用$25a + 15b = -5$减去$15b + 9a = -21$可得：$25a + 15b-(15b + 9a)=-5-(-21)$，
即$25a + 15b - 15b - 9a = -5 + 21$，$16a = 16$，解得$a = 1$。
把$a = 1$代入$5a + 3b = -1$，得$5\times1 + 3b = -1$，
即$5 + 3b = -1$，$3b = -6$，解得$b = -2$。
把$a = 1$，$b = -2$代入$a + 4b - 5$得：$1 + 4\times(-2)-5 = 1 - 8 - 5 = -12$。
D

1. 不等式组$ \left\{ \begin{array} { l } { 3 x ＞ 2 x + 3, } \\ { x ＞ m } \end{array} \right. 的解集是 x ＞ 3 $,则m的取值范围是______.

答案： - 对不等式$3x＞2x + 3$进行求解，根据不等式的基本性质，在不等式两边同时减去$2x$，得到$3x-2x＞2x + 3-2x$，即$x＞3$。
- 已知不等式组$\begin{cases}3x＞2x + 3\\x＞m\end{cases}$，其中一个不等式的解是$x＞3$，另一个不等式是$x＞m$。
- 根据“同大取大”的原则来确定不等式组的解集，因为不等式组的解集是$x＞3$，这意味着$3$要大于或等于$m$，即$m\leqslant3$。
1.$m\leqslant3$

2. 如图,标有相同字母的物体的质量相同,若A的质量为20克,则当B的质量为______克时,天平处于平衡.

答案： 先对该方程进行化简：
$2\times20 + x=20 + 3x$，即$40+x = 20+3x$。
移项可得：$3x - x=40 - 20$。
合并同类项：$2x=20$。
解得$x = 10$。
$10$

3. 一个n边形剪去一个角后,得到的一个多边形的内角和是$ 720 ^ { \circ } $,则$ n = $______.

答案： **步骤一：求出剪去一个角后多边形的边数**
设内角和为$720^{\circ}$的多边形的边数是$m$，根据多边形内角和公式：$(m - 2)\times180^{\circ}$（$m\geqslant 3$且$m$为整数），可得方程$(m - 2)\times180 = 720$，
解方程：
$\begin{aligned}(m - 2)\times180&= 720\\m - 2&= 720\div180\\m - 2&= 4\\m&= 4 + 2\\m&= 6\end{aligned}$
即剪去一个角后得到的多边形是六边形。
**步骤二：分情况讨论原$n$边形的边数**
一个$n$边形剪去一个角后，边数可能增加$1$，可能不变，也可能减少$1$，分以下三种情况进行讨论：
- **情况一：当边数增加$1$时**
此时$n + 1 = 6$，解得$n = 6 - 1 = 5$。
- **情况二：当边数不变时**
此时$n = 6$。
- **情况三：当边数减少$1$时**
此时$n - 1 = 6$，解得$n = 6 + 1 = 7$。
综上，$n$的值为$5$或$6$或$7$。
$5$或$6$或$7$

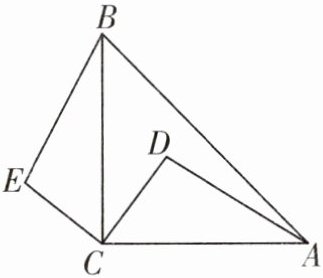
4. 如图,在等腰直角三角形ABC中,$ \angle A C B = 90 ^ { \circ } $,D为$ \triangle A B C $内一点,将线段CD绕点C逆时针旋转$ 90 ^ { \circ } $后得到CE,连结BE,若$ \angle A B E 的度数为 80 ^ { \circ } $,则$ \angle B A D $的度数为______.

答案： 本题可先证明$\triangle BCE\cong\triangle ACD$，再结合等腰直角三角形的性质求出$\angle BAD$的度数。
步骤一：证明$\triangle BCE\cong\triangle ACD$
已知$\angle ACB = 90^{\circ}$，$\angle DCE = 90^{\circ}$，所以$\angle ACB-\angle DCB=\angle DCE-\angle DCB$，即$\angle ACD=\angle BCE$。
因为线段$CD$绕点$C$逆时针旋转$90^{\circ}$后得到$CE$，所以$CD = CE$。
又因为$\triangle ABC$是等腰直角三角形，$\angle ACB = 90^{\circ}$，所以$CA = CB$。
根据全等三角形判定定理（$SAS$：两边及其夹角对应相等的三角形是全等三角形），可得$\triangle BCE\cong\triangle ACD$，则$\angle CBE=\angle CAD$。
步骤二：求出$\angle ABC$和$\angle BAC$的度数
因为$\triangle ABC$是等腰直角三角形，$\angle ACB = 90^{\circ}$，根据等腰直角三角形的性质：等腰直角三角形的两个底角相等且都等于$45^{\circ}$，所以$\angle ABC=\angle BAC = 45^{\circ}$。
步骤三：计算$\angle BAD$的度数
已知$\angle ABE = 80^{\circ}$，则$\angle CBE=\angle ABE-\angle ABC = 80^{\circ}-45^{\circ}=35^{\circ}$。
因为$\angle CBE=\angle CAD$，所以$\angle CAD = 35^{\circ}$。
那么$\angle BAD=\angle BAC-\angle CAD = 45^{\circ}-35^{\circ}=10^{\circ}$。
$10^{\circ}$

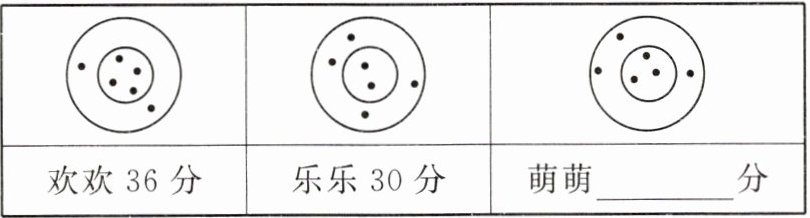
5. 欢欢、乐乐和萌萌三个人玩飞镖游戏,各投6支飞镖,规定在同一圆环内得分相同,三人中靶和得分情况如图,则萌萌得______分.

答案： $33$