《2025年快乐暑假天天练七年级数学生物》

1. 已知实数 $ a,b,c $ 满足 $ a + b + c ＞ 0,b + c = a,a + b = c $,则()
A. $ a ＞ 0,b ＞ 0,c ＞ 0 $
B. $ a ＞ 0,b = 0,c ＞ 0 $
C. $ a ＜ 0,b = 0,c ＜ 0 $
D. $ a ＜ 0,b ＞ 0,c ＜ 0 $

答案： **步骤一：根据已知条件求出$a$、$b$、$c$之间的关系**
已知$b + c = a$，$a + b = c$，将$b + c = a$代入$a + b + c ＞ 0$可得：
$a + a＞ 0$，即$2a＞ 0$，两边同时除以$2$，解得$a＞ 0$。
将$a + b = c$代入$a + b + c ＞ 0$可得：
$c + c＞ 0$，即$2c＞ 0$，两边同时除以$2$，解得$c＞ 0$。
将$b + c = a$与$a + b = c$相加可得：
$b + c + a + b = a + c$，移项可得$2b = 0$，两边同时除以$2$，解得$b = 0$。
**步骤二：得出结论**
由上述计算可知$a＞ 0$，$b = 0$，$c＞ 0$。
B

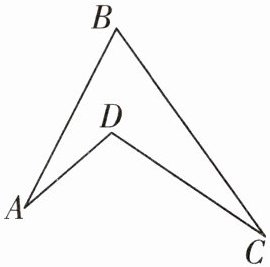
2. 我们通常称形如燕尾的几何图形为“燕尾形”. 如图是一个“燕尾形”. 已知 $ \angle ADC = 105^{\circ},\angle ABC = 63^{\circ},\angle BAD = 22^{\circ} $,则 $ \angle BCD $ 的度数为()

A. $ 63^{\circ} $
B. $ 20^{\circ} $
C. $ 85^{\circ} $
D. $ 105^{\circ} $

答案： 根据三角形外角性质：三角形的一个外角等于与它不相邻的两个内角之和。
在$\triangle ABE$中，$\angle DEC=\angle BAD + \angle ABC$（三角形外角性质），已知$\angle BAD = 22^{\circ}$，$\angle ABC = 63^{\circ}$，则$\angle DEC=22^{\circ}+63^{\circ}=85^{\circ}$。
在$\triangle DCE$中，$\angle ADC=\angle DEC+\angle BCD$（三角形外角性质），已知$\angle ADC = 105^{\circ}$，$\angle DEC = 85^{\circ}$，则$\angle BCD=\angle ADC-\angle DEC$，即$\angle BCD = 105^{\circ}-85^{\circ}=20^{\circ}$。
B

3. 一个两位数,个位数字与十位数字的和是 9,如果将个位数字与十位数字对调后所得的新数比原数大 9,则原来的两位数为()
A. 54
B. 27
C. 72
D. 45

答案： 已知个位数字与十位数字的和是$9$，则$x + y = 9$。
原来的两位数为$10x + y$，将个位数字与十位数字对调后所得的新数为$10y + x$，又因为新数比原数大$9$，所以可得方程$(10y + x)-(10x + y)=9$，化简这个方程：
$\begin{aligned}10y + x - 10x - y&=9\\9y - 9x&=9\\y - x&=1\end{aligned}$
联立方程组$\begin{cases}x + y = 9\\y - x = 1\end{cases}$，将两式相加消去$x$可得：
$\begin{aligned}x + y + y - x&=9 + 1\\2y&=10\\y&=5\end{aligned}$
把$y = 5$代入$x + y = 9$，可得$x = 9 - 5 = 4$。
所以原来的两位数是$10\times4 + 5 = 45$。
D

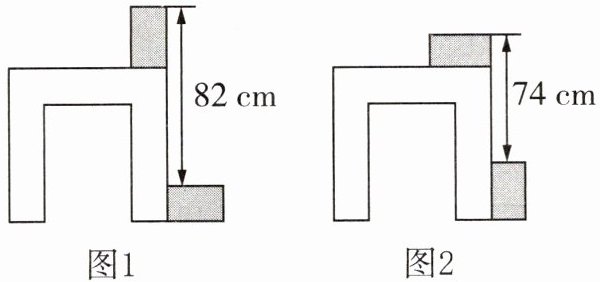
4. 老师利用两块大小一样的长方体木块测量一张桌子的高度,首先按照图 1 方式放置,再交换两木块的位置,按照图 2 方式放置,测量的数据如图,则桌子的高度是()

A. $ 77 \mathrm{cm} $
B. $ 78 \mathrm{cm} $
C. $ 79 \mathrm{cm} $
D. $ 80 \mathrm{cm} $

答案： 根据图$1$可得：$h + x - y = 82$ ①；
根据图$2$可得：$h + y - x = 74$ ②；
①$+$②得：$(h + x - y)+(h + y - x)=82 + 74$，
去括号得：$h + x - y + h + y - x = 156$，
合并同类项得：$2h = 156$，
解得：$h = 78$。
B