6. 酷爱思考的可培同学在学习了平面镶嵌的知识后,决定为家里的房子选择一些不同样式的瓷砖来铺设地板,在以下正多边形组合中,不能铺满地面的是()
A. 正八边形和正方形
B. 正五边形和正八边形
C. 正六边形和正三角形
D. 正三角形和正方形
A. 正八边形和正方形
B. 正五边形和正八边形
C. 正六边形和正三角形
D. 正三角形和正方形
答案:
**选项A:正八边形和正方形**
正八边形的每个内角为$135^{\circ}$,正方形的每个内角是$90^{\circ}$。设用$x$个正八边形和$y$个正方形可以铺满地面,则$135x + 90y = 360$,当$x = 2$,$y = 1$时,方程成立,所以正八边形和正方形能铺满地面。
**选项B:正五边形和正八边形**
正五边形每个内角是$108^{\circ}$,正八边形的每个内角为$135^{\circ}$。设用$m$个正五边形和$n$个正八边形可以铺满地面,则$108m + 135n = 360$,整理可得$12m + 15n = 40$。因为$m$、$n$为正整数,此方程无正整数解,所以正五边形和正八边形不能铺满地面。
**选项C:正六边形和正三角形**
正六边形的每个内角是$120^{\circ}$,正三角形的每个内角是$60^{\circ}$。设用$a$个正六边形和$b$个正三角形可以铺满地面,则$120a + 60b = 360$,当$a = 1$,$b = 4$或$a = 2$,$b = 2$时方程成立,所以正六边形和正三角形能铺满地面。
**选项D:正三角形和正方形**
正三角形的每个内角是$60^{\circ}$,正方形的每个内角是$90^{\circ}$。设用$c$个正三角形和$d$个正方形可以铺满地面,则$60c + 90d = 360$,当$c = 3$,$d = 2$时方程成立,所以正三角形和正方形能铺满地面。
B
正八边形的每个内角为$135^{\circ}$,正方形的每个内角是$90^{\circ}$。设用$x$个正八边形和$y$个正方形可以铺满地面,则$135x + 90y = 360$,当$x = 2$,$y = 1$时,方程成立,所以正八边形和正方形能铺满地面。
**选项B:正五边形和正八边形**
正五边形每个内角是$108^{\circ}$,正八边形的每个内角为$135^{\circ}$。设用$m$个正五边形和$n$个正八边形可以铺满地面,则$108m + 135n = 360$,整理可得$12m + 15n = 40$。因为$m$、$n$为正整数,此方程无正整数解,所以正五边形和正八边形不能铺满地面。
**选项C:正六边形和正三角形**
正六边形的每个内角是$120^{\circ}$,正三角形的每个内角是$60^{\circ}$。设用$a$个正六边形和$b$个正三角形可以铺满地面,则$120a + 60b = 360$,当$a = 1$,$b = 4$或$a = 2$,$b = 2$时方程成立,所以正六边形和正三角形能铺满地面。
**选项D:正三角形和正方形**
正三角形的每个内角是$60^{\circ}$,正方形的每个内角是$90^{\circ}$。设用$c$个正三角形和$d$个正方形可以铺满地面,则$60c + 90d = 360$,当$c = 3$,$d = 2$时方程成立,所以正三角形和正方形能铺满地面。
B
1. 一个正多边形的一个内角恰好是一个外角的4倍,则这个正多边形是正______边形.
答案:
十
2. 要使五边形木架(用5根木条钉成)不变形,至少要再钉______根木条.
答案:
$2$
3. 如图,在△ABC中,$ AB = 9 $,$ AC = 7 $,AD为中线,则△ABD与△ACD的周长之差为______.

答案:
**步骤一:分别表示出$\triangle ABD$与$\triangle ACD$的周长**
根据三角形周长的定义:三角形的周长是三角形三边长度之和。
- $\triangle ABD$的周长为$AB + BD + AD$。
- $\triangle ACD$的周长为$AC + CD + AD$。
**步骤二:求$\triangle ABD$与$\triangle ACD$的周长之差**
用$\triangle ABD$的周长减去$\triangle ACD$的周长可得:
$(AB + BD + AD)-(AC + CD + AD)$
去括号得:$AB + BD + AD - AC - CD - AD$
合并同类项得:$AB - AC + BD - CD$
**步骤三:根据中线的性质化简上式**
因为$AD$为中线,根据中线的定义:三角形的中线是连接三角形顶点和它的对边中点的线段,所以$D$为$BC$的中点,即$BD = CD$。
将$BD = CD$代入$AB - AC + BD - CD$可得:$AB - AC + BD - BD = AB - AC$。
**步骤四:代入$AB$与$AC$的值计算结果**
已知$AB = 9$,$AC = 7$,将其代入$AB - AC$可得:$9 - 7 = 2$。
$2$
根据三角形周长的定义:三角形的周长是三角形三边长度之和。
- $\triangle ABD$的周长为$AB + BD + AD$。
- $\triangle ACD$的周长为$AC + CD + AD$。
**步骤二:求$\triangle ABD$与$\triangle ACD$的周长之差**
用$\triangle ABD$的周长减去$\triangle ACD$的周长可得:
$(AB + BD + AD)-(AC + CD + AD)$
去括号得:$AB + BD + AD - AC - CD - AD$
合并同类项得:$AB - AC + BD - CD$
**步骤三:根据中线的性质化简上式**
因为$AD$为中线,根据中线的定义:三角形的中线是连接三角形顶点和它的对边中点的线段,所以$D$为$BC$的中点,即$BD = CD$。
将$BD = CD$代入$AB - AC + BD - CD$可得:$AB - AC + BD - BD = AB - AC$。
**步骤四:代入$AB$与$AC$的值计算结果**
已知$AB = 9$,$AC = 7$,将其代入$AB - AC$可得:$9 - 7 = 2$。
$2$
4. 某广场的地面是由相同的正五边形与相同的四角星形(四个尖角的度数相同)铺成的无缝隙、不重叠的图形,如图是该广场地面的一部分,则图中四角星形的尖角$ ∠ABC $的度数为______.
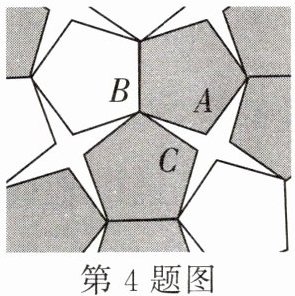

答案:
首先求正五边形内角:
- 根据多边形内角和公式$(n - 2)\times180^{\circ}$($n$为边数,$n\geqslant 3$且$n$为整数),对于正五边形,$n = 5$,则其内角和为$(5 - 2)\times180^{\circ}=540^{\circ}$。
- 因为正五边形的$5$个内角都相等,所以每个内角$\angle BCD=\frac{(5 - 2)\times180^{\circ}}{5}=108^{\circ}$。
- 然后求$\angle CBD$:
- 由图可知,在点$B$处,围绕一点的角的和为$360^{\circ}$,$\angle CBD$与正五边形内角$\angle BCD$相关。
- 因为$\angle CBD = 360^{\circ}-2\times108^{\circ}=144^{\circ}$。
- 最后求$\angle ABC$:
- 在$\triangle ABC$中(四角星形的一个角部分),$\angle ABC=\frac{180^{\circ}-\angle CBD}{2}$(四角星形四个尖角度数相同,利用三角形内角和$180^{\circ}$以及对称性)。
- 把$\angle CBD = 144^{\circ}$代入可得$\angle ABC=\frac{180^{\circ}-144^{\circ}}{2}=36^{\circ}$。
$36^{\circ}$
- 根据多边形内角和公式$(n - 2)\times180^{\circ}$($n$为边数,$n\geqslant 3$且$n$为整数),对于正五边形,$n = 5$,则其内角和为$(5 - 2)\times180^{\circ}=540^{\circ}$。
- 因为正五边形的$5$个内角都相等,所以每个内角$\angle BCD=\frac{(5 - 2)\times180^{\circ}}{5}=108^{\circ}$。
- 然后求$\angle CBD$:
- 由图可知,在点$B$处,围绕一点的角的和为$360^{\circ}$,$\angle CBD$与正五边形内角$\angle BCD$相关。
- 因为$\angle CBD = 360^{\circ}-2\times108^{\circ}=144^{\circ}$。
- 最后求$\angle ABC$:
- 在$\triangle ABC$中(四角星形的一个角部分),$\angle ABC=\frac{180^{\circ}-\angle CBD}{2}$(四角星形四个尖角度数相同,利用三角形内角和$180^{\circ}$以及对称性)。
- 把$\angle CBD = 144^{\circ}$代入可得$\angle ABC=\frac{180^{\circ}-144^{\circ}}{2}=36^{\circ}$。
$36^{\circ}$
1. 如图,在△ABC中,BD是AC边上的高,$ ∠A = 72^{\circ} $,CE平分$ ∠ACB $交BD于点E,$ ∠BEC = 115^{\circ} $,求$ ∠ABC $的度数.


答案:
因为$BD$是$AC$边上的高,所以$\angle ADB = 90^{\circ}$。
在$\triangle ABD$中,根据三角形内角和为$180^{\circ}$,可得$\angle ABD=180^{\circ}-\angle A - \angle ADB$,已知$\angle A = 72^{\circ}$,$\angle ADB = 90^{\circ}$,则$\angle ABD = 180^{\circ}-72^{\circ}-90^{\circ}=18^{\circ}$。
因为$\angle BEC$是$\triangle BED$的外角,根据三角形外角性质:三角形的一个外角等于与它不相邻的两个内角之和,所以$\angle BEC=\angle EDB+\angle ECD$。
已知$\angle BEC = 115^{\circ}$,$\angle EDB = 90^{\circ}$,则$\angle ECD=\angle BEC-\angle EDB=115^{\circ}-90^{\circ}=25^{\circ}$。
因为$CE$平分$\angle ACB$,所以$\angle ACB = 2\angle ECD$,即$\angle ACB=2\times25^{\circ}=50^{\circ}$。
在$\triangle ABC$中,根据三角形内角和为$180^{\circ}$,可得$\angle ABC=180^{\circ}-\angle A-\angle ACB$,把$\angle A = 72^{\circ}$,$\angle ACB = 50^{\circ}$代入,得$\angle ABC=180^{\circ}-72^{\circ}-50^{\circ}=58^{\circ}$。
$\angle ABC$的度数为$58^{\circ}$。
在$\triangle ABD$中,根据三角形内角和为$180^{\circ}$,可得$\angle ABD=180^{\circ}-\angle A - \angle ADB$,已知$\angle A = 72^{\circ}$,$\angle ADB = 90^{\circ}$,则$\angle ABD = 180^{\circ}-72^{\circ}-90^{\circ}=18^{\circ}$。
因为$\angle BEC$是$\triangle BED$的外角,根据三角形外角性质:三角形的一个外角等于与它不相邻的两个内角之和,所以$\angle BEC=\angle EDB+\angle ECD$。
已知$\angle BEC = 115^{\circ}$,$\angle EDB = 90^{\circ}$,则$\angle ECD=\angle BEC-\angle EDB=115^{\circ}-90^{\circ}=25^{\circ}$。
因为$CE$平分$\angle ACB$,所以$\angle ACB = 2\angle ECD$,即$\angle ACB=2\times25^{\circ}=50^{\circ}$。
在$\triangle ABC$中,根据三角形内角和为$180^{\circ}$,可得$\angle ABC=180^{\circ}-\angle A-\angle ACB$,把$\angle A = 72^{\circ}$,$\angle ACB = 50^{\circ}$代入,得$\angle ABC=180^{\circ}-72^{\circ}-50^{\circ}=58^{\circ}$。
$\angle ABC$的度数为$58^{\circ}$。
查看更多完整答案,请扫码查看


