1. 如图,方格纸上每个小方格的边长都是1,$\triangle ABC与\triangle A_{1}B_{1}C_{1}$成中心对称。
(1)画出对称中心$O$。
(2)画出将$\triangle A_{1}B_{1}C_{1}$向上平移6个单位长度得到的$\triangle A_{2}B_{2}C_{2}$。
(3)$\triangle A_{2}B_{2}C_{2}绕点C_{2}$按顺时针方向至少旋转多少度,才能与$\triangle CC_{1}C_{2}$重合?

(1)画出对称中心$O$。
(2)画出将$\triangle A_{1}B_{1}C_{1}$向上平移6个单位长度得到的$\triangle A_{2}B_{2}C_{2}$。
(3)$\triangle A_{2}B_{2}C_{2}绕点C_{2}$按顺时针方向至少旋转多少度,才能与$\triangle CC_{1}C_{2}$重合?

答案:
(1) 连接$AA_{1}$、$CC_{1}$,它们的交点就是对称中心$O$。因为成中心对称的两个图形,对应点连线都经过对称中心,且被对称中心平分。
(2) 根据平移的性质,将$\triangle A_{1}B_{1}C_{1}$的每个顶点向上平移$6$个单位长度,然后顺次连接各顶点,得到$\triangle A_{2}B_{2}C_{2}$。
(3) 观察图形可知,$\triangle A_{2}B_{2}C_{2}$中$C_{2}A_{2}=C_{2}C = 3$,$C_{2}B_{2}=C_{2}C_{1}= 4$,$\angle A_{2}C_{2}B_{2}=\angle CC_{2}C_{1} = 90^{\circ}$。所以$\triangle A_{2}B_{2}C_{2}$绕点$C_{2}$按顺时针方向至少旋转$90$度,才能与$\triangle CC_{1}C_{2}$重合。
(1) 连接$AA_{1}$、$CC_{1}$,交点$O$即为对称中心(图略)。
(2) 按平移性质画出$\triangle A_{2}B_{2}C_{2}$(图略)。
(3)$90$度。
(1) 连接$AA_{1}$、$CC_{1}$,它们的交点就是对称中心$O$。因为成中心对称的两个图形,对应点连线都经过对称中心,且被对称中心平分。
(2) 根据平移的性质,将$\triangle A_{1}B_{1}C_{1}$的每个顶点向上平移$6$个单位长度,然后顺次连接各顶点,得到$\triangle A_{2}B_{2}C_{2}$。
(3) 观察图形可知,$\triangle A_{2}B_{2}C_{2}$中$C_{2}A_{2}=C_{2}C = 3$,$C_{2}B_{2}=C_{2}C_{1}= 4$,$\angle A_{2}C_{2}B_{2}=\angle CC_{2}C_{1} = 90^{\circ}$。所以$\triangle A_{2}B_{2}C_{2}$绕点$C_{2}$按顺时针方向至少旋转$90$度,才能与$\triangle CC_{1}C_{2}$重合。
(1) 连接$AA_{1}$、$CC_{1}$,交点$O$即为对称中心(图略)。
(2) 按平移性质画出$\triangle A_{2}B_{2}C_{2}$(图略)。
(3)$90$度。
2. 已知:$\angle MON = 40^{\circ}$,$OE平分\angle MON$,点$A$,$B$,$C分别是射线OM$,$OE$,$ON$上的动点($A$,$B$,$C不与点O$重合),连结$AC交射线OE于点D$。

(1)如图1,若$AB // ON$,则
①$\angle ABO$的度数是______;
②当$\angle BAD = \angle ABD$时,$\angle OAC = $______;当$\angle BAD = \angle BDA$时,$\angle OAC = $______。
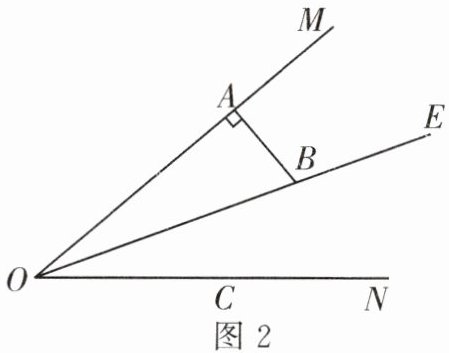
(2)如图2,若$AB \perp OM$,则是否存在$\angle OAC$,使得$\triangle ADB$中有两个相等的角?若存在,求出$\angle OAC$的度数;若不存在,说明理由。


(1)如图1,若$AB // ON$,则
①$\angle ABO$的度数是______;
②当$\angle BAD = \angle ABD$时,$\angle OAC = $______;当$\angle BAD = \angle BDA$时,$\angle OAC = $______。
(2)如图2,若$AB \perp OM$,则是否存在$\angle OAC$,使得$\triangle ADB$中有两个相等的角?若存在,求出$\angle OAC$的度数;若不存在,说明理由。
答案:
(1)①$20^{\circ}$;②$120^{\circ}$;$60^{\circ}$。
(2)存在,$\angle OAC$的度数为$20^{\circ}$或$35^{\circ}$或$50^{\circ}$。
(1)①$20^{\circ}$;②$120^{\circ}$;$60^{\circ}$。
(2)存在,$\angle OAC$的度数为$20^{\circ}$或$35^{\circ}$或$50^{\circ}$。
查看更多完整答案,请扫码查看


