《2025年快乐暑假天天练七年级数学生物》

1. 若关于$x的方程(a - 5)x^{|a| - 4} + 2025 = 0$是一元一次方程,则$a = $____.

答案： 一元一次方程指只含有一个未知数，未知数的最高次数为$1$且两边都为整式的等式。
对于方程$(a - 5)x^{|a| - 4} + 2025 = 0$，因为它是一元一次方程，所以$x$的最高次数$\vert a\vert - 4 = 1$，且$x$的系数$a - 5\neq 0$。
求解$\vert a\vert - 4 = 1$：
移项可得$\vert a\vert = 1 + 4 = 5$，那么$a = \pm 5$。
结合$a - 5\neq 0$进行判断：
由$a - 5\neq 0$可得$a\neq 5$。
综合以上两个条件，$a = - 5$。
$-5$

2. 若$x = 3是方程4x + 2m = 14$的解,则$m = $____.

答案： $1$

3. 当$x = $____时,代数式$3(x - 1)与2(x + 1)$的值互为相反数.

答案： 去括号得：$3x-3 + 2x+2 = 0$。
合并同类项得：$5x-1 = 0$。
移项得：$5x = 1$。
系数化为$1$得：$x=\frac{1}{5}$。
$\frac{1}{5}$

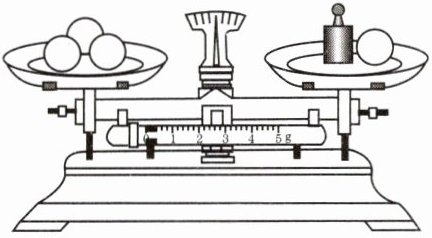
4. 如图,天平左边托盘上放着3个乒乓球,右边托盘上放着5g的砝码和1个乒乓球,天平恰好平衡. 如果设1个乒乓球的质量为$x$g,由题意你所列出的一个含有未知数$x$的方程是____.

答案： 已知设$1$个乒乓球的质量为$x$克，天平左边托盘上放着$3$个乒乓球，则左边乒乓球的总质量为$3x$克；
天平右边托盘上放着$5$克的砝码和$1$个乒乓球，那么右边的总质量为$(5 + x)$克；
因为天平恰好平衡，这意味着天平左右两边的质量相等，所以可列出方程$3x=5 + x$。
$3x = 5 + x$

解方程
1. $x - 2 = x - (2x - 1)$； 2. $x - \frac{x + 2}{3} = 1 - \frac{x - 3}{2}$；

答案： 2. 对于方程$x - \frac{x + 2}{3} = 1 - \frac{x - 3}{2}$，先去分母，方程两边同时乘以$6$，得到$6x - 2(x + 2) = 6 - 3(x - 3)$，再去括号得$6x - 2x - 4 = 6 - 3x + 9$，接着移项，将含$x$的项移到等号左边，常数项移到等号右边，得到$6x - 2x + 3x = 6 + 9 + 4$，合并同类项得$7x = 19$，最后系数化为$1$，两边同时除以$7$，解得$x=\frac{19}{7}$。
1. $x=\frac{3}{2}$ 2. $x=\frac{19}{7}$

1. 用一元一次方程解决下列问题：
山东淄博陶瓷历史悠久,享有“淄博陶瓷,当代国窑”的美誉. 某陶瓷器厂烧制陶瓷茶具,每套茶具由1个茶壶和6只茶杯组成,用1千克瓷泥可做3个茶壶或9只茶杯. 现要用6千克瓷泥全部制作这类茶具,则用多少千克瓷泥做茶壶时,恰好使制作的茶壶和茶杯配套？

答案： 设用$x$千克瓷泥做茶壶，则用$(6 - x)$千克瓷泥做茶杯。
已知$1$千克瓷泥可做$3$个茶壶，那么$x$千克瓷泥可做$3x$个茶壶；$1$千克瓷泥可做$9$只茶杯，那么$(6 - x)$千克瓷泥可做$9(6 - x)$只茶杯。
因为每套茶具由$1$个茶壶和$6$只茶杯组成，要使茶壶和茶杯配套，则茶杯数量是茶壶数量的$6$倍，可列方程：
$6\times3x = 9(6 - x)$
去括号得：$18x = 54 - 9x$
移项得：$18x + 9x = 54$
合并同类项得：$27x = 54$
系数化为$1$得：$x = 2$
用$2$千克瓷泥做茶壶时，恰好使制作的茶壶和茶杯配套。