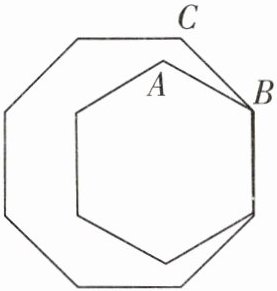
5. 如图,正八边形和正六边形的一边重合,则$\angle ABC$的度数为()
A. $10^{\circ}$
B. $15^{\circ}$
C. $20^{\circ}$
D. $25^{\circ}$

A. $10^{\circ}$
B. $15^{\circ}$
C. $20^{\circ}$
D. $25^{\circ}$
答案:
首先求正八边形内角:
- 根据多边形内角和公式$(n - 2)\times180^{\circ}$($n\geqslant 3$且$n$为整数),正八边形内角和为$(8 - 2)\times180^{\circ}=1080^{\circ}$。
- 那么正八边形每个内角为$\frac{(8 - 2)\times180^{\circ}}{8}=135^{\circ}$。
- 然后求正六边形内角:
- 正六边形内角和为$(6 - 2)\times180^{\circ}=720^{\circ}$。
- 正六边形每个内角为$\frac{(6 - 2)\times180^{\circ}}{6}=120^{\circ}$。
- 最后求$\angle ABC$:
- 由图可知$\angle ABC = 135^{\circ}-120^{\circ}=15^{\circ}$。
B
- 根据多边形内角和公式$(n - 2)\times180^{\circ}$($n\geqslant 3$且$n$为整数),正八边形内角和为$(8 - 2)\times180^{\circ}=1080^{\circ}$。
- 那么正八边形每个内角为$\frac{(8 - 2)\times180^{\circ}}{8}=135^{\circ}$。
- 然后求正六边形内角:
- 正六边形内角和为$(6 - 2)\times180^{\circ}=720^{\circ}$。
- 正六边形每个内角为$\frac{(6 - 2)\times180^{\circ}}{6}=120^{\circ}$。
- 最后求$\angle ABC$:
- 由图可知$\angle ABC = 135^{\circ}-120^{\circ}=15^{\circ}$。
B
1. 若$x < y$,则$-\frac{x}{2}$______$-\frac{y}{2}$(填“$>$”或“$<$”)。
答案:
$>$
2. 请写出一个是轴对称,但不是中心对称的几何图形名称:______。
答案:
等腰三角形
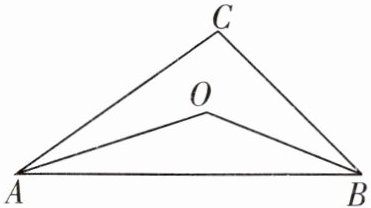
3. 如图,已知$\angle ACB = 100^{\circ}$,$OA平分\angle BAC$,$OB平分\angle ABC$,则$\angle AOB = $______$^{\circ}$。

答案:
本题可先根据三角形内角和定理求出$\angle BAC+\angle ABC$的度数,再结合角平分线的性质求出$\angle OAB+\angle OBA$的度数,最后根据三角形内角和定理求出$\angle AOB$的度数。
**步骤一:求$\angle BAC+\angle ABC$的度数**
在$\triangle ABC$中,根据三角形内角和定理:三角形内角和为$180^{\circ}$,已知$\angle ACB = 100^{\circ}$,则$\angle BAC+\angle ABC=180^{\circ}-\angle ACB = 180^{\circ}- 100^{\circ}=80^{\circ}$。
**步骤二:求$\angle OAB+\angle OBA$的度数**
因为$OA$平分$\angle BAC$,$OB$平分$\angle ABC$,根据角平分线的性质:角平分线将一个角分成两个相等的角,所以$\angle OAB=\frac{1}{2}\angle BAC$,$\angle OBA=\frac{1}{2}\angle ABC$。
则$\angle OAB+\angle OBA=\frac{1}{2}(\angle BAC+\angle ABC)=\frac{1}{2}\times80^{\circ} = 40^{\circ}$。
**步骤三:求$\angle AOB$的度数**
在$\triangle AOB$中,根据三角形内角和定理,$\angle AOB = 180^{\circ}-(\angle OAB+\angle OBA)=180^{\circ}- 40^{\circ}=140^{\circ}$。
$140$
**步骤一:求$\angle BAC+\angle ABC$的度数**
在$\triangle ABC$中,根据三角形内角和定理:三角形内角和为$180^{\circ}$,已知$\angle ACB = 100^{\circ}$,则$\angle BAC+\angle ABC=180^{\circ}-\angle ACB = 180^{\circ}- 100^{\circ}=80^{\circ}$。
**步骤二:求$\angle OAB+\angle OBA$的度数**
因为$OA$平分$\angle BAC$,$OB$平分$\angle ABC$,根据角平分线的性质:角平分线将一个角分成两个相等的角,所以$\angle OAB=\frac{1}{2}\angle BAC$,$\angle OBA=\frac{1}{2}\angle ABC$。
则$\angle OAB+\angle OBA=\frac{1}{2}(\angle BAC+\angle ABC)=\frac{1}{2}\times80^{\circ} = 40^{\circ}$。
**步骤三:求$\angle AOB$的度数**
在$\triangle AOB$中,根据三角形内角和定理,$\angle AOB = 180^{\circ}-(\angle OAB+\angle OBA)=180^{\circ}- 40^{\circ}=140^{\circ}$。
$140$
4. 已知方程组$\begin{cases}a_{1}x + b_{1}y = c_{1},\\a_{2}x + b_{2}y = c_{2}\end{cases}的解是\begin{cases}x = 3,\\y = 4,\end{cases}则方程组\begin{cases}a_{1}(x + 3) + b_{1}(y - 2) = c_{1},\\a_{2}(x + 3) + b_{2}(y - 2) = c_{2}\end{cases}$的解是______。
答案:
$\begin{cases}x = 0\\y = 6\end{cases}$
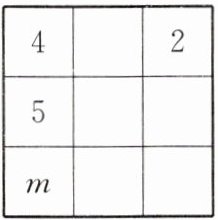
5. 传说“九宫图”是远古时代洛河中的一个神龟背上的图案,故又称“龟背图”,中国古代数学史上经常研究这一神话。数学上的“九宫图”所体现的是一个$3 × 3$表格,每一行的三个数、每一列的三个数、斜对角的三个数之和都相等,也称为三阶幻方。如图是一个满足条件的三阶幻方的一部分,则图中字母$m$表示的数是______。

答案:
因为每一行、每一列、斜对角的三个数之和都相等。
先看第一列和第一行:$4 + 5 + m=4 + a + 2$,即$9 + m=6 + a$,所以$a=m + 3$。
再看第一行和斜对角(从左上角到右下角):$4 + a + 2=4 + 5 + d$,把$a=m + 3$代入可得$4+(m + 3)+2=4 + 5 + d$,解得$d=m$。
又因为第一列和斜对角(从右上角到左下角):$4 + 5 + m=2 + b + m$,解得$b = 7$。
此时看第二行和第三列:$5 + b + d=2 + b + m$,把$b = 7$,$d=m$代入,等式恒成立。
再看第一行和第二列(设第二行中间数为$e$):$4+(m + 3)+2=5 + e+(m)$,解得$e = 4$。
最后看第一列:$4+5+m=(m + 3)+4+2$,等式恒成立,或者看第一行和第三行:$4+(m + 3)+2=m + c + m$,因为$a=m + 3$,$e = 4$,根据每一行和相等,第一行和为$4+(m + 3)+2=m + 9$,第三行$m + c + m=m + 9$,又因为$c$的值不影响,我们还可以用第一列和第二行:$4 + 5 + m=5+4 + 7$,解得$m = 7$。
$7$
先看第一列和第一行:$4 + 5 + m=4 + a + 2$,即$9 + m=6 + a$,所以$a=m + 3$。
再看第一行和斜对角(从左上角到右下角):$4 + a + 2=4 + 5 + d$,把$a=m + 3$代入可得$4+(m + 3)+2=4 + 5 + d$,解得$d=m$。
又因为第一列和斜对角(从右上角到左下角):$4 + 5 + m=2 + b + m$,解得$b = 7$。
此时看第二行和第三列:$5 + b + d=2 + b + m$,把$b = 7$,$d=m$代入,等式恒成立。
再看第一行和第二列(设第二行中间数为$e$):$4+(m + 3)+2=5 + e+(m)$,解得$e = 4$。
最后看第一列:$4+5+m=(m + 3)+4+2$,等式恒成立,或者看第一行和第三行:$4+(m + 3)+2=m + c + m$,因为$a=m + 3$,$e = 4$,根据每一行和相等,第一行和为$4+(m + 3)+2=m + 9$,第三行$m + c + m=m + 9$,又因为$c$的值不影响,我们还可以用第一列和第二行:$4 + 5 + m=5+4 + 7$,解得$m = 7$。
$7$
查看更多完整答案,请扫码查看


