《2025年快乐暑假天天练七年级数学生物》

5. 如图,将长为$5\mathrm{c}\mathrm{m}$,宽为$3\mathrm{c}\mathrm{m}的长方形ABCD先向右平移2\mathrm{c}\mathrm{m}$,再向下平移$1\mathrm{c}\mathrm{m}$,得到长方形$A'B'C'D'$,则阴影部分的面积为()

A. $6\mathrm{c}{\mathrm{m}}^{\mathrm{2}}$
B. $9\mathrm{c}{\mathrm{m}}^{\mathrm{2}}$
C. $18\mathrm{c}{\mathrm{m}}^{\mathrm{2}}$
D. $24\mathrm{c}{\mathrm{m}}^{\mathrm{2}}$

答案： 本题可先求出阴影部分长方形的长与宽，再根据长方形面积公式计算阴影部分面积。
- **步骤一：分析平移后长方形的边长变化**
已知长方形$ABCD$长为$5cm$，宽为$3cm$，向右平移$2cm$，再向下平移$1cm$得到长方形$A'B'C'D'$。
根据平移的性质可知，空白部分长方形的长为$(5 - 2)cm$，宽为$(3 - 1)cm$。
- **步骤二：计算阴影部分面积**
阴影部分面积等于两个大长方形面积之和减去$2$倍空白部分长方形面积。
根据长方形面积公式$S = 长\times宽$，大长方形$ABCD$（或$A'B'C'D'$）面积为$5\times3 = 15cm^{2}$，空白部分长方形面积为$(5 - 2)\times(3 - 1)=3\times2 = 6cm^{2}$。
则阴影部分面积$S = 2\times15-2\times6 = 30 - 12 = 18cm^{2}$。
C

6. 如图,在$\triangle ABC$中,$∠CAB= 70^{\circ }$,在同一平面内,将$\triangle ABC绕点A逆时针旋转\alpha 得到\triangle AB'C'$,且$C'C// AB$,则$\alpha $的度数为()
A. $20^{\circ }$
B. $35^{\circ }$
C. $40^{\circ }$
D. $55^{\circ }$

答案： 因为$\triangle ABC$绕点$A$逆时针旋转$\alpha$得到$\triangle AB'C'$，所以$AC = AC'$，$\angle CAC'=\alpha$。
根据等腰三角形的性质，$\angle AC'C=\angle ACC'$。
因为$C'C// AB$，$\angle CAB = 70^{\circ}$，所以$\angle ACC'=\angle CAB = 70^{\circ}$（两直线平行，内错角相等）。
在$\triangle ACC'$中，根据三角形内角和为$180^{\circ}$，可得$\angle CAC'=180^{\circ}-\angle AC'C - \angle ACC'$。
又因为$\angle AC'C=\angle ACC' = 70^{\circ}$，所以$\alpha=\angle CAC'=180^{\circ}-70^{\circ}-70^{\circ}=40^{\circ}$。
C

1. 如图,在正方形网格中,线段$A'B'是线段AB绕某点逆时针旋转\alpha $得到的,点$A'与点A$对应,则$\alpha $的度数为______.

答案： **步骤一：确定旋转中心**
连接$AA'$、$BB'$，分别作$AA'$、$BB'$的垂直平分线，两条垂直平分线的交点即为旋转中心$O$。
通过观察正方形网格可知，旋转中心$O$是网格线的交点。
**步骤二：求出旋转角$\alpha$的度数**
根据旋转的性质可知，对应点与旋转中心所连线段的夹角等于旋转角，所以$\angle AOA'$就是旋转角$\alpha$。
在正方形网格中，通过观察可知$\angle AOA' = 90^{\circ}$，即$\alpha = 90^{\circ}$。
$90^{\circ}$

2. 如图,在已知的$\triangle ABC$中,按以下步骤作图：①分别以$B$,$C$为圆心,以大于$\frac {1}{2}BC$的长为半径作弧,两弧相交于点$M$,$N$；②作直线$MN交AB于点D$,连结$CD$.若$AC= 3$,$AB= 9$,则$\triangle ACD$的周长为______.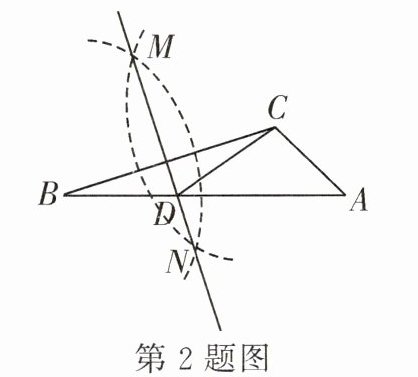

答案： $\triangle ACD$的周长为$AC + AD+CD$，因为$BD = CD$，所以$\triangle ACD$的周长$=AC + AD + BD=AC + AB$。
已知$AC = 3$，$AB = 9$，则$\triangle ACD$的周长为$3 + 9=12$。
$12$