1. 在$\triangle ABC$中,若$AB = 5$,$BC = 12$,则边$AC$的长可能是()
A. 3
B. 4
C. 7
D. 8
A. 3
B. 4
C. 7
D. 8
答案:
D
2. 检测游泳池的水质,要求三次检验的$pH的平均值不小于7.2$,且不大于$7.8$。已知第一次$pH检测值为7.4$,第二次$pH检测值在7.0至7.9$之间(包含$7.0和7.9$),若该游泳池检测合格,则第三次$pH检测值x$的范围是()
A. $7.2\leqslant x\leqslant 8.1$
B. $7.1\leqslant x\leqslant 8.0$
C. $7.2\leqslant x\leqslant 8.0$
D. $7.1\leqslant x\leqslant 8.1$
A. $7.2\leqslant x\leqslant 8.1$
B. $7.1\leqslant x\leqslant 8.0$
C. $7.2\leqslant x\leqslant 8.0$
D. $7.1\leqslant x\leqslant 8.1$
答案:
**步骤一:根据平均值的计算公式列出不等式组**
已知三次检验的$pH$平均值不小于$7.2$,且不大于$7.8$,第一次$pH$检测值为$7.4$,第二次$pH$检测值在$7.0$至$7.9$之间(包含$7.0$和$7.9$),第三次$pH$检测值为$x$。
根据平均值的计算公式:平均值$=$总和$\div$个数,可得三次检验的$pH$平均值为$\dfrac{7.4 + 第二次检测值 + x}{3}$。
因为平均值不小于$7.2$,且不大于$7.8$,所以可列出不等式组$\begin{cases}\dfrac{7.4 + 7.0 + x}{3} \geqslant 7.2\\\dfrac{7.4 + 7.9 + x}{3} \leqslant 7.8\end{cases}$。
**步骤二:分别求解不等式组中的两个不等式**
- 解不等式$\dfrac{7.4 + 7.0 + x}{3} \geqslant 7.2$:
不等式两边同时乘以$3$可得:$7.4 + 7.0 + x \geqslant 7.2\times3$,即$14.4 + x \geqslant 21.6$。
不等式两边同时减去$14.4$可得:$x \geqslant 21.6 - 14.4$,即$x \geqslant 7.2$。
- 解不等式$\dfrac{7.4 + 7.9 + x}{3} \leqslant 7.8$:
不等式两边同时乘以$3$可得:$7.4 + 7.9 + x \leqslant 7.8\times3$,即$15.3 + x \leqslant 23.4$。
不等式两边同时减去$15.3$可得:$x \leqslant 23.4 - 15.3$,即$x \leqslant 8.1$。
**步骤三:确定不等式组的解集**
综合以上两个不等式的解$x \geqslant 7.2$和$x \leqslant 8.1$,可得不等式组的解集为$7.2\leqslant x\leqslant 8.1$,即第三次$pH$检测值$x$的范围是$7.2\leqslant x\leqslant 8.1$。
A
已知三次检验的$pH$平均值不小于$7.2$,且不大于$7.8$,第一次$pH$检测值为$7.4$,第二次$pH$检测值在$7.0$至$7.9$之间(包含$7.0$和$7.9$),第三次$pH$检测值为$x$。
根据平均值的计算公式:平均值$=$总和$\div$个数,可得三次检验的$pH$平均值为$\dfrac{7.4 + 第二次检测值 + x}{3}$。
因为平均值不小于$7.2$,且不大于$7.8$,所以可列出不等式组$\begin{cases}\dfrac{7.4 + 7.0 + x}{3} \geqslant 7.2\\\dfrac{7.4 + 7.9 + x}{3} \leqslant 7.8\end{cases}$。
**步骤二:分别求解不等式组中的两个不等式**
- 解不等式$\dfrac{7.4 + 7.0 + x}{3} \geqslant 7.2$:
不等式两边同时乘以$3$可得:$7.4 + 7.0 + x \geqslant 7.2\times3$,即$14.4 + x \geqslant 21.6$。
不等式两边同时减去$14.4$可得:$x \geqslant 21.6 - 14.4$,即$x \geqslant 7.2$。
- 解不等式$\dfrac{7.4 + 7.9 + x}{3} \leqslant 7.8$:
不等式两边同时乘以$3$可得:$7.4 + 7.9 + x \leqslant 7.8\times3$,即$15.3 + x \leqslant 23.4$。
不等式两边同时减去$15.3$可得:$x \leqslant 23.4 - 15.3$,即$x \leqslant 8.1$。
**步骤三:确定不等式组的解集**
综合以上两个不等式的解$x \geqslant 7.2$和$x \leqslant 8.1$,可得不等式组的解集为$7.2\leqslant x\leqslant 8.1$,即第三次$pH$检测值$x$的范围是$7.2\leqslant x\leqslant 8.1$。
A
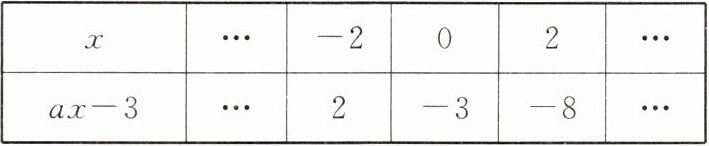
3. 若代数式$ax - 3$的值如表,则关于$x的一元一次方程ax - 3 = 0$的解在如图数轴上表示的对应点是()
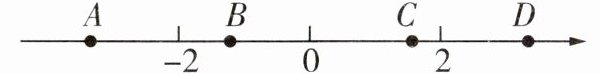
A. $A$
B. $B$
C. $C$
D. $D$

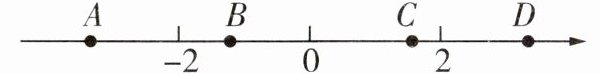
A. $A$
B. $B$
C. $C$
D. $D$
答案:
首先,把$x = 0$代入$ax - 3$,可得$a\times0 - 3=-3$,这符合表格中$x = 0$时$ax - 3$的值。
然后,把$x=-2$代入$ax - 3$得$-2a - 3 = 2$,
移项可得$-2a=2 + 3$,
即$-2a = 5$,
解得$a=-\frac{5}{2}$。
所以方程$ax - 3 = 0$为$-\frac{5}{2}x-3 = 0$,
移项得$-\frac{5}{2}x=3$,
两边同时乘以$-\frac{2}{5}$,$x=3\times(-\frac{2}{5})=-\frac{6}{5}=-1.2$。
$-1.2$在数轴上对应的点是$B$点。
B
然后,把$x=-2$代入$ax - 3$得$-2a - 3 = 2$,
移项可得$-2a=2 + 3$,
即$-2a = 5$,
解得$a=-\frac{5}{2}$。
所以方程$ax - 3 = 0$为$-\frac{5}{2}x-3 = 0$,
移项得$-\frac{5}{2}x=3$,
两边同时乘以$-\frac{2}{5}$,$x=3\times(-\frac{2}{5})=-\frac{6}{5}=-1.2$。
$-1.2$在数轴上对应的点是$B$点。
B
4. 某校七年级有$3$个班,已知一班、二班的平均人数与三班人数之和为$45$,二班、三班的平均人数与一班人数之和为$48$,一班、三班的平均人数与二班人数之和为$47$,则三个班的总人数为()
A. 68
B. 70
C. 72
D. 74
A. 68
B. 70
C. 72
D. 74
答案:
根据“一班、二班的平均人数与三班人数之和为$45$”可得$\frac{x + y}{2}+z = 45$,即$x + y+2z = 90$ ①;
根据“二班、三班的平均人数与一班人数之和为$48$”可得$\frac{y + z}{2}+x = 48$,即$2x + y+z = 96$ ②;
根据“一班、三班的平均人数与二班人数之和为$47$”可得$\frac{x + z}{2}+y = 47$,即$x + 2y+z = 94$ ③。
①$+$②$+$③可得:$(x + y+2z)+(2x + y+z)+(x + 2y+z)=90 + 96+94$,
$4x + 4y + 4z = 280$,两边同时除以$4$得$x + y + z = 70$,即三个班的总人数为$70$人。
B
根据“二班、三班的平均人数与一班人数之和为$48$”可得$\frac{y + z}{2}+x = 48$,即$2x + y+z = 96$ ②;
根据“一班、三班的平均人数与二班人数之和为$47$”可得$\frac{x + z}{2}+y = 47$,即$x + 2y+z = 94$ ③。
①$+$②$+$③可得:$(x + y+2z)+(2x + y+z)+(x + 2y+z)=90 + 96+94$,
$4x + 4y + 4z = 280$,两边同时除以$4$得$x + y + z = 70$,即三个班的总人数为$70$人。
B
5. 某商场重新装修后准备在大厅的主楼梯上铺设一种红色的地毯,已知这种地毯的批发价为每平方米$40$元,且知主楼梯道的宽为$3m$,其侧面如图所示,则买地毯至少需要()

A. 1881.6元
B. 768元
C. 1008元
D. 672元

A. 1881.6元
B. 768元
C. 1008元
D. 672元
答案:
本题可通过平移的性质求出地毯的长度,再结合楼梯道的宽求出地毯的面积,最后根据单价求出总价。
步骤一:计算地毯的长度
根据平移的性质,将楼梯的水平线段向上平移,竖直线段向右平移,可发现地毯的长度等于楼梯横向长度与纵向长度之和。
已知楼梯纵向长度$AC = 2.8m$,横向长度$BC = 5.6m$,所以地毯的长度为$2.8 + 5.6=8.4m$。
步骤二:计算地毯的面积
已知楼梯道的宽为$3m$,根据长方形面积公式$S = 长\times宽$,可得地毯的面积为$8.4×3 = 25.2$平方米。
步骤三:计算买地毯所需的费用
已知地毯的批发价为每平方米$40$元,根据“总价$=$单价$\times$数量”,可得买地毯至少需要$25.2×40 = 1008$元。
C
步骤一:计算地毯的长度
根据平移的性质,将楼梯的水平线段向上平移,竖直线段向右平移,可发现地毯的长度等于楼梯横向长度与纵向长度之和。
已知楼梯纵向长度$AC = 2.8m$,横向长度$BC = 5.6m$,所以地毯的长度为$2.8 + 5.6=8.4m$。
步骤二:计算地毯的面积
已知楼梯道的宽为$3m$,根据长方形面积公式$S = 长\times宽$,可得地毯的面积为$8.4×3 = 25.2$平方米。
步骤三:计算买地毯所需的费用
已知地毯的批发价为每平方米$40$元,根据“总价$=$单价$\times$数量”,可得买地毯至少需要$25.2×40 = 1008$元。
C
查看更多完整答案,请扫码查看


