《2025年海淀单元测试AB卷八年级物理下册人教版》

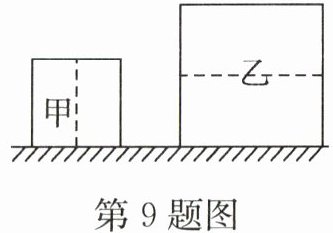
9.（2024·临沂兰陵期末）如图所示，实心均匀正方体甲、乙对水平地面的压强均为 $p_0$，若沿竖直方向切去甲的一半，沿水平方向切去乙的一半，此时它们对地面的压强为 $p_{甲}$ 和 $p_{乙}$，则下列判断正确的是（ ）

A. $p_{甲}=p_{乙}$
B. $p_{甲}＜p_{乙}$
C. $p_{甲}=p_{0}$
D. $p_{乙}=p_{0}$

答案： C

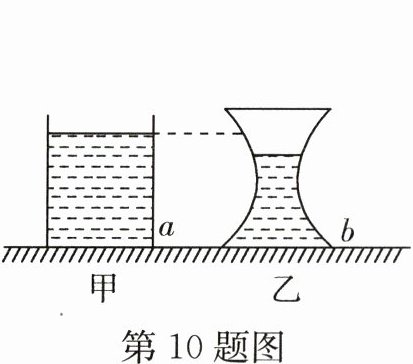
10. 如图所示，水平桌面上有甲、乙两个质量相同的薄壁容器.两个容器开口大小相同、底面积相同，分别装有质量相同的 $a$、$b$两种液体，两个容器中的液面高度不同.下列说法正确的是（ ）

A. 两种液体密度的大小关系是 $\rho_{a}＞\rho_{b}$
B. 桌面对两个容器支持力的大小关系是 $F_{甲}＞F_{乙}$
C. 两种液体对容器底部压强的大小关系是 $p_{a}＜p_{b}$
D. 两个容器对桌面压强的大小关系是 $p_{甲}＜p_{乙}$

答案： C [解析]因为甲、乙两个容器中液体的质量相同，但甲中液体的体积大于乙中液体的体积，所以甲中液体的密度小于乙中液体的密度，即ρₐ ＜ ρᵦ，A错误；因为两个容器放在水平桌面上，所以容器对桌面的压力大小等于容器的重力与液体的重力之和，而两个容器的质量和容器内液体的质量均相同，所以两个容器对桌面的压力大小相等，再根据力的作用是相互的可知，桌面对两个容器支持力的大小相等，B错误；由图可知，甲中液体对容器底部的压力与液体的重力相等，乙中液体对容器底部的压力大于液体的重力，由于两容器中液体的质量相同，则甲中液体对容器底部的压力小于乙中液体对容器底部的压力，两容器的底面积相同，根据p = $\frac{F}{S}$可知，甲中液体对容器底部的压强小于乙中液体对容器底部的压强，即pₐ ＜ pᵦ，C正确；因为两个容器对桌面的压力大小相等，且容器的底面积相同，根据p = $\frac{F}{S}$可知，两个容器对桌面的压强大小相等，D错误.

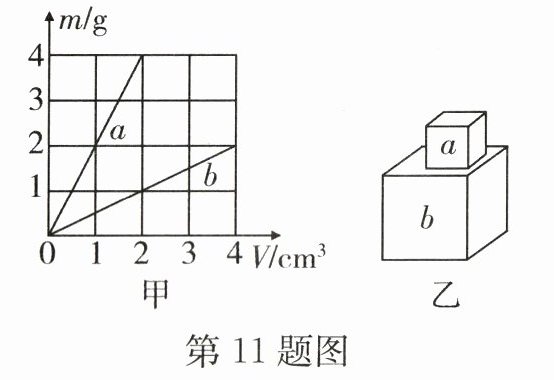
11. 图甲是 $a$、$b$两种物质的质量与体积的关系图像，分别用 $a$、$b$两种物质制成的两个实心正方体的边长之比为1∶2.将它们按图乙方式叠放在水平地面上时，$a$对 $b$ 的压强和 $b$对地面的压强之比为（ ）


A. 4∶3
B. 3∶4
C. 1∶2
D. 2∶1

答案： A [解析]根据图甲可知，当mₐ = 4 g时，Vₐ = 2 cm³，当mᵦ = 2 g时，Vᵦ = 4 cm³，则a、b的密度之比$\frac{ρₐ}{ρᵦ}$ = $\frac{\frac{mₐ}{Vₐ}}{\frac{mᵦ}{Vᵦ}}$ = $\frac{mₐVᵦ}{mᵦVₐ}$ = $\frac{4 g×4 cm³}{2 g×2 cm³}$ = $\frac{4}{1}$；用a、b两种物质制成的两个实心正方体的边长之比为1∶2，则两个实心正方体的底面积之比$\frac{Sₐ}{Sᵦ}$ = $\frac{1}{4}$，体积之比$\frac{Vₐ'}{Vᵦ'}$ = $\frac{1}{8}$；两个实心正方体的重力之比$\frac{Gₐ}{Gᵦ}$ = $\frac{mₐg}{mᵦg}$ = $\frac{ρₐVₐ'g}{ρᵦVᵦ'g}$ = $\frac{1}{2}$，a对b的压强和b对地面的压强之比$\frac{pₐ}{pᵦ}$ = $\frac{\frac{Fₐ}{Sₐ}}{\frac{Fₐ + Fᵦ}{Sᵦ}}$ = $\frac{\frac{Gₐ}{Sₐ}}{\frac{Gₐ + Gᵦ}{Sᵦ}}$ = $\frac{GₐSᵦ}{(Gₐ + Gᵦ)Sₐ}$ = $\frac{1×4}{(1 + 2)×1}$ = $\frac{4}{3}$.

12.〔学科融合〕（多选）以下文字选自朱自清的《春》：“小草偷偷地从土里钻出来，嫩嫩的，绿绿的……坐着，躺着，打两个滚，踢几脚球……”关于文中所涉及的现象解释正确的是（ ）
A. “小草偷偷地从土里钻出来”，草对土有力的作用
B. “坐着，躺着”，由坐到躺，人对地面的压强变小
C. “打两个滚”，在草地上滚动，人不受摩擦力
D. “踢几脚球”，踢出的球由于具有惯性能继续运动

答案： ABD [解析]“小草偷偷地从土里钻出来”，草改变了土的形状，所以草对土有力的作用，A正确；“坐着，躺着”，由坐到躺，压力不变，受力面积变大，人对地面的压强变小，B正确；人在草地上滚动，受到一个与其运动方向相反的摩擦力，C错误；任何物体都具有惯性，踢出的球由于具有惯性仍能继续运动，D正确.