《2025年寒假零距离七年级数学北师大版》

20. 如图所示，已知∠AOB = 90°，∠EOF = 60°，OE平分∠AOB，OF平分∠BOC，求∠AOC和∠BOC的度数.

答案： 解：因为OE平分∠AOB，∠AOB＝90°，所以∠BOE＝45°. 又∠EOF＝60°，所以∠BOF＝15°. 又因为OF平分∠BOC，所以∠BOC＝30°，∠AOC＝90°＋30°＝120°.

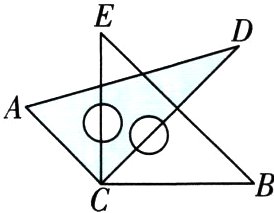
21. 如图所示，将两块三角板的直角顶点重合.
（1）写出以C为顶点的相等的角；
（2）若∠ACB = 150°，求∠DCE的度数；
（3）写出∠ACB与∠DCE之间所具有的数量关系；
（4）当三角板ACD绕点C旋转时，你所写出的（3）中的关系是否变化？请说明理由.

答案： 解：
(1)∠ACD＝∠BCE，∠ACE＝∠BCD.
(2)∠DCE＝30°.
(3)∠ACB＋∠DCE＝180°.
(4)不变. 理由略.

22. 如图，七年级小林同学在一张透明纸上画了一条长8cm的线段MN，并在线段MN上任意找了一个不同于M、N的点C，然后用折纸的方法找出了线段MC、NC的中点A和B，并求出了线段AB的长为4cm. 回答：
（1）小林是如何找到线段MC、NC的中点的？又是如何求出线段AB的长为4cm的？
（2）在反思解题过程时，小林想到：如果点C在线段MN的延长线上，“AB = 4cm”这一结论还成立吗？请你帮小林画出图形，并解决这一问题.

答案： 解：
(1)纸是透明的，小林将纸对折，依次使点M、C重合，点N、C重合，两个折痕与线段MN的交点就分别是中点A和B，AB＝AC＋BC＝$\frac{1}{2}MC+\frac{1}{2}NC=\frac{1}{2}MN=\frac{1}{2}\times8 = 4$(cm).
(2)成立，理由：如图，
若点C在线段MN的延长线上，AB＝AC－BC＝$\frac{1}{2}MC-\frac{1}{2}NC=\frac{1}{2}(MC - NC)=\frac{1}{2}MN=\frac{1}{2}\times8 = 4$(cm).