《2025年寒假零距离七年级数学北师大版》

14. 喜欢集邮的小慧共有中外邮票145张，其中中国邮票的张数比外国邮票的张数的2倍少5张，问小慧有中国邮票________张，外国邮票________张.

答案： 95 50

15. 甲每小时走$a$千米，乙每小时走$b$千米（$a＞b$），若两人同时同地出发，(1)反向行走$x$小时后，两人相距________千米；(2)同向行走$y$小时后，两人相距________千米；(3)他们从A地出发，到达相距$x$千米的B地，若甲比乙早到2小时，则题中的一个等量关系是__________.

答案：
(1) $(ax + bx)$
(2) $(ay - by)$
(3) $\frac{x}{a} + 2 = \frac{x}{b}$

16. 解方程：
(1)$3x - 6 = -15 - 6x$；
(2)$\frac{4}{3}x + 5 = x - 17$；
(3)$6(3x + 1)-2(4x - 1)=2(x + 2)-1$；
(4)$\frac{x}{3}+\frac{13 - x}{2}=5$.

答案： 解：
(1) 移项，得 $3x + 6x = -15 + 6$. 合并同类项，得 $9x = -9$. 方程两边除以 9，得 $x = -1$；
(2) 移项，得 $\frac{4}{3}x - x = -17 - 5$. 合并同类项，得 $\frac{1}{3}x = -22$. 方程两边同乘 3，得 $x = -66$；
(3) 去括号，得 $18x + 6 - 8x + 2 = 2x + 4 - 1$，移项得 $18x - 8x - 2x = 4 - 1 - 2 - 6$，合并同类项，得 $8x = -5$，系数化为 1，得 $x = -\frac{5}{8}$；
(4) 去分母，得 $2x + 3(13 - x) = 30$，去括号，得 $2x + 39 - 3x = 30$，移项，得 $2x - 3x = 30 - 39$，合并同类项，得 $-x = -9$，系数化为 1，得 $x = 9$.

17. 如果$x = -3$是方程$-3x^{2}-ax - 7 = -19$的解，那么$x =\frac{4}{3}$是这个方程的解吗？请说明理由.

答案： 解：因为 $x = -3$ 是方程 $-3x^{2} - ax - 7 = -19$ 的解，所以 $-3×(-3)^{2} - a(-3) - 7 = -19$，即 $a = 5$，则原方程为：$-3x^{2} - 5x - 7 = -19$，当 $x = \frac{4}{3}$ 时，左边 $= -3×(\frac{4}{3})^{2} - 5×\frac{4}{3} - 7 = -19 =$ 右边，所以 $x = \frac{4}{3}$ 是这个方程的解.

18. 若关于$x$的方程$\frac{x - k}{2}=k - 3x$和$2x - 3 = 1$有相同的解，求$k$的值.

答案： 解：由 $2x - 3 = 1$ 得 $x = 2$，把 $x = 2$ 代入方程 $\frac{x - k}{2} = k - 3x$ 得 $\frac{2 - k}{2} = k - 6$，解得 $k = \frac{14}{3}$.

19. 某同学在解方程$2(x - a)=-5(3x - 1)+1$去括号时，右边的括号忘记乘-5，解得$x = 2$，求$a$的值以及原方程正确的解.

答案： 解：把 $x = 2$ 代入 $2(x - a) = (3x - 1) + 1$ 中，得 $a = -1$，把 $a = -1$ 代入 $2(x - a) = -5(3x - 1) + 1$ 中，得 $2(x + 1) = -5(3x - 1) + 1$，解得 $x = \frac{4}{17}$.

20. 某小组8名同学参加一次知识竞赛，共答10道题，每题分值相同. 每题答对得分，答错或不答扣分. 各同学的得分情况如下表：

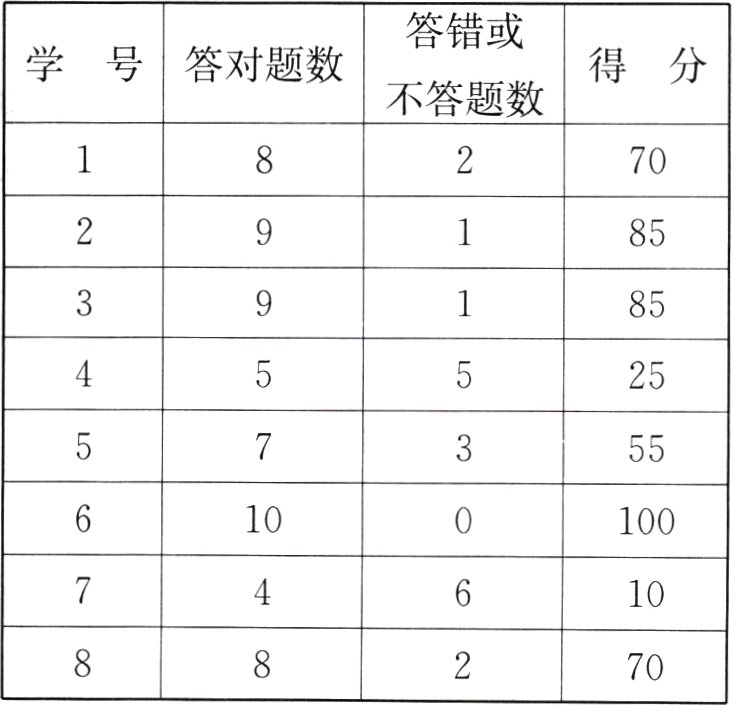
(1)如果答对的题数为$n$（$n$在1到10之间，且为整数），用含$n$的式子表示得分；
(2)在什么情况下得分为零分？在什么情况下得分为负分？

答案： 解：由 6 号同学知，每答对一题 10 分. 设答错或不答一题扣 $x$ 分，那么从 1 号同学的数据可列方程：$8×10 - 2x = 70$，解得 $x = 5$. 所以答错或不答一题扣 5 分.
(1) 如果答对的题数为 $n$，那么得分为 $10n - 5(10 - n)$，即 $15n - 50$.
(2) 如果得分为零分，那么解方程 $15n - 50 = 0$，得 $n = \frac{10}{3}$. 因为竞赛题目数不可能是 $\frac{10}{3}$，所以在任何情况下都不可能得零分；因为答对题越少得分越少，所以当答对题数小于 $\frac{10}{3}$，即答对题数为 0，1，2，3 时，得分为负分.